当前仅显示指定条件回帖 [ 展开查看全部 ]
文件名称:
深度学习优化方法知识点.md
所在目录:
深度学习基础
文件大小:
78.23 KB
下载地址:
文本预览:
# 目录
- [1.有哪些方法能提升CNN模型的泛化能力](#user-content-1有哪些方法能提升cnn模型的泛化能力)
- [2.BN层面试高频问题大汇总](#user-content-2bn层面试高频问题大汇总)
- [3.Instance Normalization的作用](#user-content-3instance-normalization的作用)
- [4.有哪些提高GAN训练稳定性的Tricks](#user-content-4有哪些提高gan训练稳定性的tricks)
- [1.输入Normalize](#user-content-1输入normalize)
- [2.替换原始的GAN损失函数和标签反转](#user-content-2替换原始的gan损失函数和标签反转)
- [3.使用具有球形结构的随机噪声$Z$作为输入](#user-content-3使用具有球形结构的随机噪声z作为输入)
- [4.使用BatchNorm](#user-content-4使用batchnorm)
- [5.避免使用ReLU,MaxPool等操作引入稀疏梯度](#user-content-5避免使用relu,maxpool等操作引入稀疏梯度)
- [6.使用Soft和Noisy的标签](#user-content-6使用soft和noisy的标签)
- [7.使用Adam优化器](#user-content-7使用adam优化器)
- [8.追踪训练失败的信号](#user-content-8追踪训练失败的信号)
- [9.在输入端适当添加噪声](#user-content-9在输入端适当添加噪声)
- [10.生成器和判别器差异化训练](#user-content-10生成器和判别器差异化训练)
- [11.Two Timescale Update Rule (TTUR)](#user-content-11two-timescale-update-rule-ttur)
- [12.Gradient Penalty (梯度惩罚)](#user-content-12gradient-penalty-(梯度惩罚))
- [13.Spectral Normalization(谱归一化)](#user-content-13spectral-normalization(谱归一化))
- [14.使用多个GAN结构](#user-content-14使用多个gan结构)
- [5.什么是超参数?有哪些常用的超参数?](#user-content-5什么是超参数?有哪些常用的超参数?)
- [6.如何寻找到最优超参数?](#user-content-6如何寻找到最优超参数?)
- [7.Spectral Normalization的相关知识](#user-content-7spectral-normalization的相关知识)
- [8.什么是EMA?](#8.什么是EMA?)
- [9.深度学习中有哪些经典的优化器?](#user-content-9深度学习中有哪些经典的优化器?)
- [10.深度学习中常用的学习率衰减策略有哪些?](#user-content-10深度学习中常用的学习率衰减策略有哪些?)
- [11.什么是方向导数?](#user-content-11什么是方向导数?)
- [12.什么是梯度](#user-content-12什么是梯度?)
- [13.为什么沿梯度方向是函数变化最快的方向?](#user-content-13为什么沿梯度方向是函数变化最快的方向?)
- [14.T5LayerNorm和LayerNorm的区别是什么?](#user-content-14T5LayerNorm和LayerNorm的区别是什么?)
- [15.什么是xavier初始化?](#user-content-15什么是xavier初始化?)
- [16.深度学习训练过程中,如果设置的学习率过大,会导致什么问题?](#user-content-16深度学习训练过程中,如果设置的学习率过大,会导致什么问题?)
- [17.介绍一下深度学习中的学习率衰减?](#user-content-17介绍一下深度学习中的学习率衰减?)
- [18.深度学习训练过程中,如果设置的学习率过小,会导致什么问题?](#user-content-18深度学习训练过程中,如果设置的学习率过小,会导致什么问题?)
- [19.深度学习中模型权重融合有哪些主流的方法?](#user-content-19深度学习中模型权重融合有哪些主流的方法?)
- [20.什么是adafactor优化器?](#user-content-20什么是adafactor优化器?)
- [21.什么是深度学习中的梯度裁剪技术?](#user-content-21什么是深度学习中的梯度裁剪技术?)
- [22.CNN+Transformer组合的架构有哪些优势?](#user-content-22CNN+Transformer组合的架构有哪些优势?)
- [23.介绍一下schedule_free优化器的原理](#user-content-23介绍一下schedule_free优化器的原理)
- [24.LayerNorm有什么作用?](#user-content-24LayerNorm有什么作用?)
- [25.AI模型权重0初始化,在训练过程中还能更新权重吗?AI模型权重0初始化有哪些优势和劣势?](#user-content-25AI模型权重0初始化,在训练过程中还能更新权重吗?AI模型权重0初始化有哪些优势和劣势?)
1. 采集更多数据:数据决定算法的上限。
2. 优化数据分布:数据类别均衡。
3. 选用合适的目标函数。
4. 设计合适的网络结构。
5. 数据增强。
6. 权值正则化。
7. 使用合适的优化器等。
BN层解决了什么问题?
统计机器学习中的一个经典假设是“源空间(source domain)和目标空间(target domain)的数据分布(distribution)是一致的”。如果不一致,那么就出现了新的机器学习问题,如transfer learning/domain adaptation等。而covariate shift就是分布不一致假设之下的一个分支问题,它是指源空间和目标空间的条件概率是一致的,但是其边缘概率不同。对于神经网络的各层输出,由于它们经过了层内卷积操作,其分布显然与各层对应的输入信号分布不同,而且差异会随着网络深度增大而增大,但是它们所能代表的label仍然是不变的,这便符合了covariate shift的定义。
因为神经网络在做非线性变换前的激活输入值随着网络深度加深,其分布逐渐发生偏移或者变动(即上述的covariate shift)。之所以训练收敛慢,一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近(比如sigmoid),所以这导致反向传播时低层神经网络的梯度消失,这是训练深层神经网络收敛越来越慢的本质原因。而BN就是通过一定的正则化手段,把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布,避免因为激活函数导致的梯度弥散问题。所以与其说BN的作用是缓解covariate shift,也可以说BN可缓解梯度弥散问题。
BN的公式

其中scale和shift是两个可学的参数,因为减去均值除方差未必是最好的分布。比如数据本身就很不对称,或者激活函数未必是对方差为1的数据有最好的效果。所以要加入缩放及平移变量来完善数据分布以达到比较好的效果。
BN层训练和测试的不同
在训练阶段,BN层是对每个batch的训练数据进行标准化,即用每一批数据的均值和方差。(每一批数据的方差和标准差不同)
而在测试阶段,我们一般只输入一个测试样本,并没有batch的概念。因此这个时候用的均值和方差是整个数据集训练后的均值和方差,可以通过滑动平均法求得:
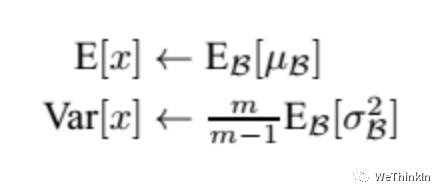
上面式子简单理解就是:对于均值来说直接计算所有batch $u$ 值的平均值;然后对于标准偏差采用每个batch $σ_B$ 的无偏估计。
在测试时,BN使用的公式是:
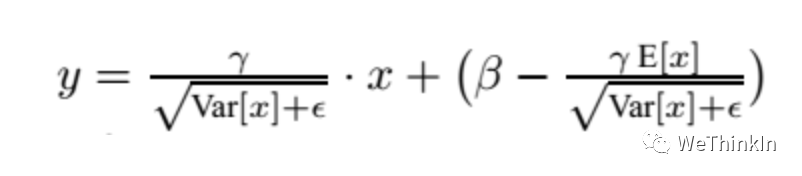
BN训练时为什么不用整个训练集的均值和方差?
因为用整个训练集的均值和方差容易过拟合,对于BN,其实就是对每一batch数据标准化到一个相同的分布,而不同batch数据的均值和方差会有一定的差别,而不是固定的值,这个差别能够增加模型的鲁棒性,也会在一定程度上减少过拟合。
BN层用在哪里?
在CNN中,BN层应该用在非线性激活函数前面。由于神经网络隐藏层的输入是上一层非线性激活函数的输出,在训练初期其分布还在剧烈改变,此时约束其一阶矩和二阶矩无法很好地缓解 Covariate Shift;而BN的分布更接近正态分布,限制其一阶矩和二阶矩能使输入到激活函数的值分布更加稳定。
BN层的参数量
我们知道 $γ$ 和 $β$ 是需要学习的参数,而BN的本质就是利用优化学习改变方差和均值的大小。在CNN中,因为网络的特征是对应到一整张特征图上的,所以做BN的时候也是以特征图为单位而不是按照各个维度。比如在某一层,特征图数量为 $c$ ,那么做BN的参数量为 $c * 2$ 。
BN的优缺点
**优点:**
1. 可以选择较大的初始学习率。因为这个算法收敛很快。
2. 可以不用dropout,L2正则化。
3. 不需要使用局部响应归一化。
4. 可以把数据集彻底打乱。
5. 模型更加健壮。
**缺点:**
1. Batch Normalization非常依赖Batch的大小,当Batch值很小时,计算的均值和方差不稳定。
2. 所以BN不适用于以下几个场景:小Batch,RNN等。
Instance Normalization(IN)和Batch Normalization(BN)一样,也是Normalization的一种方法,只是IN是作用于单张图片,而BN作用于一个Batch。
BN对Batch中的每一张图片的同一个通道一起进行Normalization操作,而IN是指单张图片的单个通道单独进行Normalization操作。如下图所示,其中C代表通道数,N代表图片数量(Batch)。
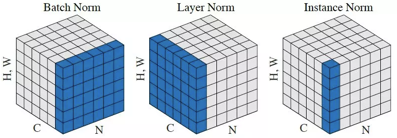
IN适用于生成模型中,比如图片风格迁移。因为图片生成的结果主要依赖于某个图像实例,所以对整个Batch进行Normalization操作并不适合图像风格化的任务,在风格迁移中使用IN不仅可以加速模型收敛,并且可以保持每个图像实例之间的独立性。
下面是IN的公式:
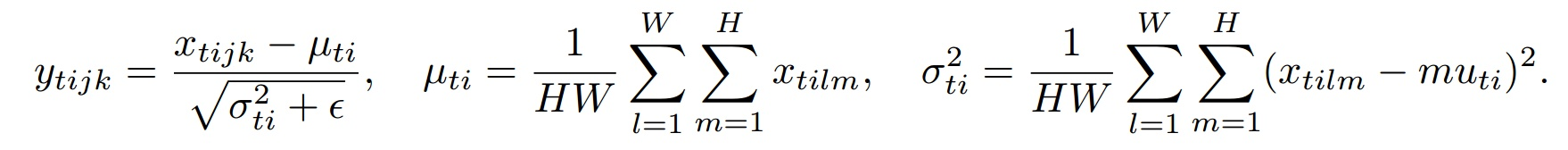
其中t代表图片的index,i代表的是feature map的index。
1. 将输入图片Normalize到 $[-1,1]$ 之间。
2. 生成器最后一层的输出使用Tanh激活函数。
Normalize非常重要,没有处理过的图片是没办法收敛的。图片Normalize一种简单的方法是(images-127.5)/127.5,然后送到判别器去训练。同理生成的图片也要经过判别器,即生成器的输出也是-1到1之间,所以使用Tanh激活函数更加合适。
1. 原始GAN损失函数会出现训练早期梯度消失和Mode collapse(模型崩溃)问题。可以使用Earth Mover distance(推土机距离)来优化。
2. 实际工程中用反转标签来训练生成器更加方便,即把生成的图片当成real的标签来训练,把真实的图片当成fake来训练。
1. 不要使用均匀分布进行采样

2. 使用高斯分布进行采样
1. 一个mini-batch中必须只有real数据或者fake数据,不要把他们混在一起训练。
2. 如果能用BatchNorm就用BatchNorm,如果不能用则用instance normalization。

1. GAN的稳定性会因为引入稀疏梯度受到很大影响。
2. 最好使用类LeakyReLU的激活函数。(D和G中都使用)
3. 对于下采样,最好使用:Average Pooling或者卷积+stride。
4. 对于上采样,最好使用:PixelShuffle或者转置卷积+stride。
最好去掉整个Pooling逻辑,因为使用Pooling会损失信息,这对于GAN训练没有益处。
1. Soft Label,即使用 $[0.7-1.2]$ 和 $[0-0.3]$ 两个区间的随机值来代替正样本和负样本的Hard Label。
2. 可以在训练时对标签加一些噪声,比如随机翻转部分样本的标签。
1. Adam优化器对于GAN来说非常有用。
2. 在生成器中使用Adam,在判别器中使用SGD。
1. 判别器的损失=0说明模型训练失败。
2. 如果生成器的损失稳步下降,说明判别器没有起作用。
1. 在判别器的输入中加入一些人工噪声。
2. 在生成器的每层中都加入高斯噪声。
1. 多训练判别器,尤其是加了噪声的时候。
对判别器和生成器使用不同的学习速度。使用较低的学习率更新生成器,判别器使用较高的学习率进行更新。
使用梯度惩罚机制可以极大增强 GAN 的稳定性,尽可能减少mode collapse问题的产生。
Spectral normalization可以用在判别器的weight normalization技术,可以确保判别器是K-Lipschitz连续的。
可以使用多个GAN/多生成器/多判别器结构来让GAN训练更稳定,提升整体效果,解决更难的问题。
### 什么是超参数?
在深度学习中,**超参数(Hyperparameters)是指在训练开始前设置的模型参数,不是通过训练学习得到的**。超参数的选择对模型性能有很大的影响,不同的超参数设置可能导致显著不同的训练结果。
### 常见的超参数包括:
1. **预处理(Data Augmentation、Normalization and Standardization)**:对输入数据进行预处理。
2. **批量大小(Batch Size)**:每次梯度更新使用的训练样本数量。
3. **学习率(Learning Rate)**:控制模型权重更新的步伐。
4. **学习率衰减(Learning Rate Decay)**:控制学习率随时间逐渐减小的方式。
5. **优化算法/优化器(Optimizer)**:如SGD、Adam、RMSprop等,控制模型权重的更新方式。
6. **损失函数(Loss Function)**:设置训练目标。
8. **迭代次数(Number of Epochs)**:训练过程中遍历整个训练集的次数。
9. **神经网络结构(Network Architecture)**:如层数、每层的神经元数量等。
10. **正则化参数(Regularization Parameters)**:如L2正则化系数、Dropout率等。
11. **激活函数(Activation Function)**:决定每个神经元的输出形式。
12. **权重初始化(Weight Initialization)**:决定模型的初始权重。
**找到最优超参数的过程通常被称为超参数优化(Hyperparameter Optimization)**。常用的方法包括以下几种:
#### 1. **手动调整(Manual Tuning)**:
手动调整超参数是最简单但最费时的方法,通常依赖于经验和试错。可以通过观察模型在验证集上的性能来逐步调整超参数。
#### 2. **网格搜索(Grid Search)**:
网格搜索是一种系统的尝试多个超参数组合的方法。
- **步骤**:
1. 定义每个超参数的可能取值范围。
2. 穷举所有可能的超参数组合。
3. 对每个组合进行交叉验证,评估模型在验证集上的性能。
4. 选择性能最好的组合作为最优超参数。
- **缺点**:计算成本高,特别是超参数数量多和取值范围大的情况下。
#### 3. **随机搜索(Random Search)**:
随机搜索是一种在超参数空间中随机采样进行尝试的方法。
- **步骤**:
1. 定义每个超参数的可能取值范围。
2. 随机采样一定数量的超参数组合。
3. 对每个组合进行交叉验证,评估模型在验证集上的性能。
4. 选择性能最好的组合作为最优超参数。
- **优点**:比网格搜索更有效率,通常在相同计算成本下能找到更好的超参数组合。
#### 4. **贝叶斯优化(Bayesian Optimization)**:
贝叶斯优化是一种利用贝叶斯统计理论的方法,通过构建超参数与模型性能之间的概率模型来选择最优超参数。
- **步骤**:
1. 选择初始点,训练模型并评估性能。
2. 构建代理模型(通常是高斯过程)来模拟超参数空间。
3. 使用代理模型选择下一个最有可能提升性能的超参数组合。
4. 训练模型并更新代理模型。
5. 重复步骤3和4,直到达到预定的迭代次数或时间限制。
- **优点**:比随机搜索和网格搜索更高效,适合高维和复杂的超参数空间。
#### 5. **遗传算法(Genetic Algorithms)**:
遗传算法是一种基于生物进化原理的优化算法。
- **步骤**:
1. 初始化一个包含多个超参数组合的种群。
2. 通过交叉和变异生成新的超参数组合。
3. 根据模型性能评估每个组合的适应度,选择适应度高的组合进行下一代繁衍。
4. 重复步骤2和3,直到达到预定的迭代次数或性能。
- **优点**:能探索复杂的超参数空间,适合解决多峰优化问题。
#### 6. **超参数调优库**:
一些开源的超参数调优库提供了自动化的超参数优化功能。
- **常见库**:
- **Hyperopt**:支持贝叶斯优化,基于TPE(Tree of Parzen Estimators)。
- **Optuna**:灵活且高效的超参数优化库,支持贝叶斯优化、随机搜索和其他自定义优化算法。
- **Ray Tune**:支持多种搜索算法和分布式超参数优化。
- **Scikit-Optimize**:基于Scikit-Learn的优化库,支持贝叶斯优化。
### 示例:使用Optuna进行超参数优化
以下是使用Optuna进行超参数优化的简单示例:
```python
import optuna
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score
# 加载数据集
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=42)
# 定义目标函数
def objective(trial):
# 定义超参数的搜索空间
C = trial.suggest_loguniform('C', 1e-5, 1e2)
gamma = trial.suggest_loguniform('gamma', 1e-5, 1e-1)
# 创建模型
model = SVC(C=C, gamma=gamma)
# 训练模型
model.fit(X_train, y_train)
# 评估模型
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
return accuracy
# 创建Optuna研究对象并进行优化
study = optuna.create_study(direction='maximize')
study.optimize(objective, n_trials=100)
# 输出最优超参数
print('Best trial:')
trial = study.best_trial
print(f' Accuracy: {trial.value}')
print(' Params: ')
for key, value in trial.params.items():
print(f' {key}: {value}')
```
通过这种方法,可以高效地寻找最优超参数组合,从而提升模型性能。
Spectral Normalization是一种wegiht Normalization技术,和weight-clipping以及gradient penalty一样,也是让模型满足1-Lipschitz条件的方式之一。
Lipschitz(利普希茨)条件限制了函数变化的剧烈程度,即函数的梯度,来确保统计的有界性。因此函数更加平滑,在神经网络的优化过程中,参数变化也会更稳定,不容易出现梯度爆炸。
Lipschitz条件的约束如下所示:

其中 $K$ 代表一个常数,即利普希茨常数。若 $K=1$ ,则是1-Lipschitz。
在GAN领域,Spectral Normalization有很多应用。在WGAN中,只有满足1-Lipschitz约束时,W距离才能转换成较好求解的对偶问题,使得WGAN更加从容的训练。
如果想让矩阵A映射: $R^{n}\to R^{m}$ 满足K-Lipschitz连续,K的最小值为 $\sqrt{\lambda_{1}}$ ( $\lambda_{1}$ 是 $A_TA$ 的最大特征值),那么要想让矩阵A满足1-Lipschitz连续,只需要在A的所有元素上同时除以 $\sqrt{\lambda_{1}}$ (Spectral norm)。
Spectral Normalization实际上在做的事,是将每层的参数矩阵除以自身的最大奇异值,本质上是一个逐层SVD的过程,但是真的去做SVD就太耗时了,所以采用幂迭代的方法求解。过程如下图所示:

得到谱范数 $\sigma_l(W)$ 后,每个参数矩阵上的参数皆除以它,以达到Normalization的目的。
EMA(指数移动平均,Exponential Moving Average)是一种在深度学习和统计领域常用的技术,特别是在参数优化和数据平滑处理中非常有用。在深度学习中,EMA 常用于模型训练过程中参数的更新,以帮助提高模型的稳定性和性能。
### EMA 的工作原理
EMA 的核心思想是对数据或参数进行加权平均,其中较新的观测值会被赋予更高的权重。这种方法可以快速反映最近的变化,同时还能保留一部分之前的信息,从而在保持数据平滑的同时减少噪声的影响。即将每次梯度更新后的权值和前一次的权重进行联系,使得本次更新收到上次权值的影响。
公式表示为:
$$EMA_t = \alpha \times x_t + (1 - \alpha) \times EMA_{t-1}$$
其中:
- $EMA_t$ 是在时间点 t 的 EMA 值。
- $x_t$ 是在时间点 t 的观测值。
- $\alpha$ 是平滑因子,通常在 0 和 1 之间。
### EMA 在深度学习中的应用
在深度学习中,EMA 可用于模型参数的更新。例如,在训练一个深度神经网络时,通过计算参数的 EMA 可以得到更稳定的模型版本。这在训练过程中尤其有用,因为它可以减少参数更新中的高频波动,从而帮助模型更好地收敛。
### 优势
使用 EMA 更新模型参数的优势包括:
- **减少过拟合**:EMA 可以平滑模型在训练过程中的表现,避免过度追踪训练数据中的噪声。
- **增强泛化能力**:通过平滑化参数更新,模型在未见数据上的表现往往更加稳定和强健。
ema版本的模型可以生成更多创意性的结果,适合训练使用
### SGD(随机梯度下降)
随机梯度下降的优化算法在科研和工业界是很常用的。
很多理论和工程问题都能转化成对目标函数进行最小化的数学问题。
举个例子:梯度下降(Gradient Descent)就好比一个人想从高山上奔跑到山谷最低点,用最快的方式奔向最低的位置。
SGD的公式:

动量(Momentum)公式:

基本的mini-batch SGD优化算法在深度学习取得很多不错的成绩。然而也存在一些问题需解决:
1. 选择恰当的初始学习率很困难。
2. 学习率调整策略受限于预先指定的调整规则。
3. 相同的学习率被应用于各个参数。
4. 高度非凸的误差函数的优化过程,如何避免陷入大量的局部次优解或鞍点。
### AdaGrad(自适应梯度)
AdaGrad优化算法(Adaptive Gradient,自适应梯度),它能够对每个不同的参数调整不同的学习率,对频繁变化的参数以更小的步长进行更新,而稀疏的参数以更大的步长进行更新。
AdaGrad公式:


$g_{t,i}$ 表示t时刻的 $\theta_{i}$ 梯度。
$G_{t,ii}$ 表示t时刻参数 $\theta_{i}$ 的梯度平方和。
与SGD的核心区别在于计算更新步长时,增加了分母:梯度平方累积和的平方根。此项能够累积各个参数 $\theta_{i}$ 的历史梯度平方,频繁更新的梯度,则累积的分母逐渐偏大,那么更新的步长相对就会变小,而稀疏的梯度,则导致累积的分母项中对应值比较小,那么更新的步长则相对比较大。
AdaGrad能够自动为不同参数适应不同的学习率(平方根的分母项相当于对学习率α进进行了自动调整,然后再乘以本次梯度),大多数的框架实现采用默认学习率α=0.01即可完成比较好的收敛。
**优势:** 在数据分布稀疏的场景,能更好利用稀疏梯度的信息,比标准的SGD算法更有效地收敛。
**缺点:** 主要缺陷来自分母项的对梯度平方不断累积,随时间的增加,分母项越来越大,最终导致学习率收缩到太小无法进行有效更新。
### RMSProp
RMSProp结合梯度平方的指数移动平均数来调节学习率的变化。能够在不稳定的目标函数情况下进行很好地收敛。
计算t时刻的梯度:

计算梯度平方的指数移动平均数(Exponential Moving Average), $\gamma$ 是遗忘因子(或称为指数衰减率),依据经验,默认设置为0.9。

梯度更新的时候,与AdaGrad类似,只是更新的梯度平方的期望(指数移动均值),其中 $\varepsilon = 10^{-8}$ ,避免除数为0。默认学习率 $\alpha = 0.001$ 。

**优势:** 能够克服AdaGrad梯度急剧减小的问题,在很多应用中都展示出优秀的学习率自适应能力。尤其在不稳定(Non-Stationary)的目标函数下,比基本的SGD、Momentum、AdaGrad表现更良好。
### Adam
Adam优化器结合了AdaGrad和RMSProp两种优化算法的优点。对梯度的一阶矩估计(First Moment Estimation,即梯度的均值)和二阶矩估计(Second Moment Estimation,即梯度的未中心化的方差)进行综合考虑,计算出更新步长。
**Adam的优势:**
1. 实现简单,计算高效,对内存需求少。
2. 参数的更新不受梯度的伸缩变换影响。
3. 超参数具有很好的解释性,且通常无需调整或仅需很少的微调。
4. 更新的步长能够被限制在大致的范围内(初始学习率)。
5. 能自然地实现步长退火过程(自动调整学习率)。
6. 很适合应用于大规模的数据及参数的场景。
7. 适用于不稳定目标函数。
8. 适用于梯度稀疏或梯度存在很大噪声的问题。
**Adam的实现原理:**

计算t时刻的梯度:

然后计算梯度的指数移动平均数, $m_{0}$ 初始化为0。
类似于Momentum算法,综合考虑之前累积的梯度动量。
$\beta_{1}$ 系数为指数衰减率,控制动量和当前梯度的权重分配,通常取接近于1的值。默认为0.9。

接着,计算梯度平方的指数移动平均数, $v_{0}$ 初始化为0。
$\beta_{2}$ 系数为指数衰减率,控制之前的梯度平方的影响情况。默认为0.999。
类似于RMSProp算法,对梯度平方进行加权均值。

由于 $m_{0}$ 初始化为0,会导致$m_{t}$偏向于0,尤其在训练初期阶段。
所以,此处需要对梯度均值$m_{t}$进行偏差纠正,降低偏差对训练初期的影响。

同时 $v_{0}$ 也要进行偏差纠正:

最后总的公式如下所示:

其中默认学习率 $\alpha = 0.001$ , $\varepsilon = 10^{-8}$ 避免除数变为0。
从表达式中可以看出,对更新的步长计算,能够从梯度均值和梯度平方两个角度进行自适应地调节,而不是直接由当前梯度决定。
**Adam的不足:**
虽然Adam算法目前成为主流的优化算法,不过在很多领域里(如计算机视觉的图像识别、NLP中的机器翻译)的最佳成果仍然是使用带动量(Momentum)的SGD来获取到的。
在AI领域中,合适的学习率调整策略对于模型的训练效果和收敛速度至关重要。
学习率衰减(或调整)是用来在训练过程中逐步减小学习率的方法,目的是帮助模型更好地收敛,避免训练过程中的振荡或不稳定。
以下是几种常用的学习率衰减方法:
### 1. 固定学习率衰减
这是最简单的衰减方法之一,其中学习率按预定的固定间隔和固定因子进行减少。例如,每过10个epoch将学习率乘以0.1。
### 2. 指数衰减
在指数衰减模式下,学习率按照指数函数逐步减小,通常定义为:
$\text{Learning Rate} = \text{Initial Learning Rate} \times e^{-\text{decay rate} \times \text{epoch}}$
其中,decay rate是一个预先设定的常数,epoch是当前的训练轮数。
### 3. 时间基衰减
时间基衰减与指数衰减类似,但学习率的衰减与训练的具体时间(通常是epoch数)更直接相关:
$\text{Learning Rate} = \frac{\text{Initial Learning Rate}}{1 + \text{decay rate} \times \text{epoch}}$
### 4. 阶梯衰减
在阶梯衰减中,学习率在一系列预设的epoch(如每20个epoch)后显著下降。这种衰减通常是手动设置的,非常直观,允许模型在较高的学习率下快速学习,并在训练后期通过较低的学习率细化模型。
### 5. 余弦衰减
余弦衰减是一种较新的策略,它模仿了余弦函数的形状来调整学习率,从初始学习率逐渐减小到接近零的值。这种方法在一些周期性或重启的训练策略中特别有效,可以帮助模型跳出局部最小值。
### 6. 适应性学习率方法
这包括像Adam和RMSprop这样的优化算法,这些算法本身就能够调整每个参数的学习率,通常基于历史梯度的平方(用于归一化梯度)。这些方法自动调整学习率,无需显式的衰减策略。
### 7. 热身和重启
- **学习率热身**:在训练初期,学习率从一个较低的值逐渐增加到设定的初始学习率。这有助于模型在训练初期稳定下来,防止初始学习率过高导致的不稳定。
- **周期性重启**:学习率按周期性地增加和减少,每次“重启”都从较高的学习率开始,然后再次衰减。这种方法有助于模型跳出局部最小值,寻找更好的全局最小值。
这些学习率调整方法可以单独使用,也可以结合使用,以达到最佳的训练效果。选择哪种衰减策略取决于具体任务、模型的复杂性以及训练数据的特点。在实际应用中,通常需要通过多次实验来确定最合适的学习率调整策略。
- 导数是二维平面中,曲线上某一点沿着x轴方向变化的速率
- 偏导数是在三维空间中,曲面上某一点沿着x轴方向或y轴方向变化的速率
- 方向导数是在三维空间中,曲面上某一点沿着任一方向的变化率
定理:如果函数 $f(x,y)$ 在点 $P_{0}\left(x_{0}, y_{0}\right)$ 可微分,那么函数在该点沿任一方向 $l$ 的方向导数存在,且有
$$\frac{\partial f}{\partial \vec{l}}=\frac{\partial f}{\partial x} \cdot \cos \alpha+\frac{\partial f}{\partial y} \cdot \cos \beta$其中$\vec{l}=\{\cos \alpha, \cos \beta\}$$
设函数 $z=f(x,y)$ 在平面区域$D$内具有一阶连续偏导数,对于区域$D$中的每一个点都可以确定一个向量 $f_{x}(x, y) \vec{i}+f_{y}(x, y) \vec{j}$ 成为函数在该点的梯度,记为:
$$\text{gradf}(\mathrm{x}, \mathrm{y})=\nabla f(x, y)= \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} = f_{x}(x, y) \vec{i}+f_{y}(x, y) \vec{j}$$
梯度下降法,是机器学习、深度学习中比较核心也是较为常用的优化算法,但为什么沿梯度方向,函数变化最快?方向导数与梯度有什么关系?
设 $\vec{e}=\{\cos \alpha, \cos \beta\}$ 是方向 $l$ 上的单位向量,则
$$\frac{\partial f}{\partial \vec{l}}=\frac{\partial f}{\partial x} \cdot \cos \alpha+\frac{\partial f}{\partial y} \cdot \cos \beta = \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} {\cos \alpha, \cos \beta\}=\text{grad} f(x, y) \cdot \vec{e}$$
$=|\text{gradf}(x, y)|\cdot\cos\theta$ ,其中 $\theta$ 为 $\text{gradf}(\mathrm{x}, \mathrm{y})$ 与 $\vec{e}$ 的夹角
1. 当 $\theta =0$ 时,即 $\vec{e}$ 沿着梯度方向,方向导数取得最大值
2. 当 $\theta = \pi/2$ 时,方向导数为0
3. 当 $\theta =\pi$ 时,即 $\vec{e}$ 沿着梯度反方向,方向导数取得最小值
## 综上
当方向导数大于0时,方向导数的大小用来描述函数上升的速率快慢,方向导数越大,表明函数上升越快,当方向导数小于0时,方向导数的大小用来描述函数下降的速率快慢,方向导数越小,表明函数下降越快,即 $\vec{e}$ 沿着梯度反方向,方向导数取得最小值,此时函数下降速率最快。
比起标准的层归一化(Layer Normalization),T5LayerNorm主要特点是只对网络的权重参数进行缩放(scale),而不进行偏移(shift)。T5LayerNorm的主要公式如下:
$$\text{T5LayerNorm}(x) = \frac{x}{\sqrt{\text{Var}(x) + \epsilon}} \times \text{weight}$$
- $x$ 是输入的张量。
- $\text{Var}(x)$ 是 $x$ 的方差,计算方式是对每个元素平方后求平均值。
- $\epsilon$ 是一个小常数,用于防止除零错误,确保数值稳定性。
- $\text{weight}$ 是一个可训练的参数,用来缩放输出。
总的来说,T5LayerNorm的关键在于:
1. **只进行缩放,不进行偏移**:它不像LayerNorm那样先减去均值再缩放,它只根据输入数据的方差进行缩放。
2. **处理方式简洁但有效**:通过对输入数据的平方均值进行归一化,T5LayerNorm保持了简洁性,并且这种归一化方式在处理较高维度的输入时非常高效。
3. **适应高维数据**:T5LayerNorm特别适用于AIGC大模型中的高维数据输入,因为它能够在保持数值稳定性的同时,减少不必要的计算量。
正是上述的这些特点使得T5LayerNorm成为AI视频大模型中非常实用的归一化方法。
Xavier初始化(也称为Glorot初始化)是深度学习中用于神经网络权重初始化的一种方法,它在训练深层神经网络时非常重要,尤其是为了避免梯度消失或梯度爆炸问题。Xavier初始化通过设置权重,使得网络层的输入和输出的方差保持一致,从而稳定梯度的传播。
在深度神经网络中,如果权重初始化得不当,随着网络的层数增加,可能会出现梯度消失(vanishing gradient)和梯度爆炸(exploding gradient)的问题。
### 1. Xavier 初始化的原理
Xavier初始化的核心思想是保持网络中的输入和输出的方差相等,以此来稳定梯度的传播。它假设激活函数是线性的,且每一层的输入和输出分布应该保持相似。
具体来说,设某一层有 $n_{\text{in}}$ 个输入神经元和 $n_{\text{out}}$ 个输出神经元,Xavier 初始化会将权重 $W$ 初始化为满足以下分布:
- **均匀分布**:权重从一个均匀分布中采样,其范围为:
$$W \sim \mathcal{U}\left(-\frac{1}{\sqrt{n_{\text{in}}}}, \frac{1}{\sqrt{n_{\text{in}}}}\right)$$
- **正态分布**:权重从一个均值为 0,标准差为 $\frac{1}{\sqrt{n_{\text{in}}}}$ 的正态分布中采样:
$$W \sim \mathcal{N}\left(0, \frac{1}{n_{\text{in}}}\right)$$
这种初始化方式保证了前向传播和反向传播时,梯度不会因为层数增加而出现消失或爆炸的情况。
### 2. Xavier 初始化的推导
在 Xavier 初始化中,目标是保持每一层输出的方差与输入的方差大致相同。假设:
- 输入 $x$ 的方差为 $\text{Var}(x) = \sigma_x^2$
- 权重 $W$ 的方差为 $\text{Var}(W) = \sigma_W^2$
在前向传播时,假设每层的输入 $x$ 具有 $n_{\text{in}}$ 个神经元,权重矩阵为 $W$ ,那么输出 $y$ 的方差应该满足以下条件:
$$\text{Var}(y) = n_{\text{in}} \cdot \text{Var}(W) \cdot \text{Var}(x)$$
为了防止参数权重的方差在传递过程中不断增大或减小,Xavier初始化的目标是让输出方差等于输入方差,即 $\text{Var}(y) = \text{Var}(x)$ 。这样可以推导出权重初始化的条件:
$$n_{\text{in}} \cdot \sigma_W^2 = 1 \quad \Rightarrow \quad \sigma_W^2 = \frac{1}{n_{\text{in}}}$$
这解释了 Xavier 初始化为什么将权重的方差设置为 $\frac{1}{n_{\text{in}}}$ 。
### 3. Xavier 初始化的适用范围
Xavier 初始化适合用于激活函数是对称且线性或接近线性的情况,例如:
- **线性激活函数**
- **双曲正切函数(tanh)**
然而,当激活函数是 ReLU 或其变体(如 Leaky ReLU)时,由于这些激活函数的非线性性质,Xavier 初始化可能不太合适。这时,通常使用 **He 初始化**,它是 Xavier 初始化的变体,专门针对 ReLU 激活函数做了调整。
### 4. Xavier 初始化的改进:He 初始化
对于非对称的激活函数(例如 ReLU),Xavier 初始化的假设可能不再成立。He 初始化专门为这些激活函数设计,公式类似于 Xavier,但调整了方差的计算:
$$W \sim \mathcal{N}(0, \frac{2}{n_{\text{in}}})$$
这种初始化方式能更好地保持梯度在深层网络中的传播。
训练过程不稳定:
当学习率过大时,会致使权重更新幅度偏大,进而使损失函数的值在每次迭代中出现剧烈起伏。如此一来,模型参数可能持续在损失函数的不同区域间跳动,引发训练过程的不稳定性,甚至可能出现发散状况。
无法收敛:
由于每次更新的步幅过大,模型或许永远无法抵达或靠近全局最优点或局部最优点。损失函数的值难以稳定在一个较低区间内,模型性能无法提升,训练也就无法实现收敛。
梯度爆炸:
采用较大学习率时,可能引发梯度爆炸问题。梯度值会变得极大,导致参数更新量极为庞大。这不但使训练变得极为艰难,还可能让参数达到极端数值,进一步加重训练的不稳定性。
性能不佳:
即便模型勉强实现收敛,最终得到的模型性能通常也不尽如人意。这是因为参数在损失函数表面跳跃幅度过大,无法精细地调整至最优解附近,致使模型的泛化能力较弱,表现不理想。
学习率衰减(learning rate decay)是深度学习模型训练过程中常用的技术,用于在训练过程中逐渐减小学习率,以帮助模型更好地收敛。常见的学习率衰减方式包括:
时间衰减(Time-based decay):按照固定的周期(epoch)或迭代次数(iteration)减小学习率。例如,每10个epoch将学习率减小一半。
指数衰减(Exponential decay):按照指数函数减小学习率。例如,每10个epoch将学习率减小为原来的0.1倍。
余弦衰减(Cosine decay):按照余弦函数减小学习率。余弦衰减在训练初期可以快速减小学习率,在训练后期可以逐渐减小学习率,有助于模型更好地收敛。
阶梯衰减(Step decay):在预定义的轮次列表处调整学习率。例如,在10、20、30个epoch后将学习率减小为原来的0.1倍。
余弦退火(Cosine annealing):余弦退火是一种特殊的余弦衰减策略,它会在训练过程中逐渐减小学习率,并在训练结束时将学习率减小到0。
学习率预热(Learning rate warmup):学习率预热是指在训练初期使用较小的学习率,随着训练的进行逐渐增大学习率。这种方法可以避免模型在训练初期由于学习率过大而发散。
学习率调整(Learning rate scheduling):根据模型的性能指标(如验证集上的损失)动态调整学习率。常见的调整策略包括学习率退火(learning rate annealing)和学习率周期调整(learning rate cycling)。
学习率优化算法(Learning rate optimizers):一些优化算法(如Adam、RMSprop等)内部包含学习率调整机制,可以在训练过程中自动调整学习率。
选择哪种学习率衰减方式取决于具体任务、模型和数据集的特点。在实际应用中,通常需要通过实验来确定最佳的学习率衰减策略。
学习率衰减过早可能引发以下几种状况:
学习率衰减过早可能带来以下情况:
一、训练进程变缓
学习率过早衰减会使模型参数更新的幅度减小,每次迭代中的权重调整变小。这会致使模型在全局最优解附近的搜索速度极为缓慢,从而大幅增加训练时间。
二、易陷局部最优
过早衰减学习率会让模型参数更新步伐变小,这样一来模型更容易被困在局部最优处,难以跳出局部最优去探寻全局最优解。原因在于较小的学习率降低了模型在损失函数表面进行大幅度搜索的能力。
三、未充分利用高学习率阶段
训练初期,较高的学习率能助力模型快速收敛以找到较优解。若学习率过早衰减,模型就无法充分发挥初始高学习率阶段的快速收敛特性,可能致使模型训练效率降低,甚至无法达到理想的初始收敛效果。
四、训练不充分
在训练早期,模型参数处于快速调整阶段。此时若学习率过早衰减,模型可能无法充分训练至较好状态,最终导致模型性能欠佳。因为早期的参数更新需要较大幅度的调整来适应复杂的损失表面结构,而过早衰减的学习率会限制这种能力。
在深度学习中,模型权重融合(Model Weight Fusion)是指将多个模型的参数(权重)进行合并或融合,旨在**提高模型的性能或实现模型压缩**。权重融合的方法在模型集成、知识蒸馏、联邦学习等场景中具有广泛应用。以下是一些主流的权重融合方法:
### 1. **简单加权平均法 (Simple Weight Averaging)**
- **原理**:通过对多个模型的权重取加权平均,生成一个融合后的新模型。
- **公式**:
$$W_{\text{fused}} = \frac{1}{N} \sum_{i=1}^N W_i$$
其中, $W_i$ 是第 $i$ 个模型的权重, $N$ 是模型的数量。
- **应用场景**:
- 联邦学习(Federated Learning):每个客户端训练本地模型,服务器通过聚合客户端模型权重来更新全局模型。
- 模型集成:结合多个相似结构的模型来生成更具鲁棒性的模型。
### 2. **线性插值法 (Linear Interpolation)**
- **原理**:给定两个模型,通过在它们的权重空间中进行线性插值生成新的模型。
- **公式**:
$$W_{\text{fused}} = \alpha W_1 + (1 - \alpha) W_2$$
其中, $W_1$ 和 $W_2$ 是两个模型的权重, $\alpha$ 是插值系数,通常取值在 $[0,1]$ 之间。
- **应用场景**:
- 在优化模型时,用于平衡两个模型之间的性能表现,特别是在权重空间中寻找局部最优解。
### 3. **逐层融合 (Layer-wise Fusion)**
- **原理**:通过逐层将多个模型的权重进行融合,而不是全局地直接对所有权重进行加权平均。
- **步骤**:
- 对应层的权重矩阵或张量进行加权平均或其他操作。
- 每层都可以使用不同的融合方法。
- **应用场景**:
- 在具有相同架构的模型之间融合时效果较好。
- 常用于知识蒸馏或模型压缩,逐层传递知识。
### 4. **基于权重相似性的融合 (Weight Similarity-based Fusion)**
- **原理**:基于多个模型的权重相似性来确定融合方式。通过计算不同模型权重的距离,调整不同模型的权重融合比例。
- **常用方法**:
- 计算每个层权重的余弦相似性(Cosine Similarity)或欧氏距离(Euclidean Distance),来确定如何调整每个模型的权重贡献。
- **应用场景**:
- 当模型结构相似但参数值差异较大时,利用权重相似性可以更智能地融合模型。
- 特别适用于使用不同数据集或不同初始化训练得到的模型。
### 5. **知识蒸馏 (Knowledge Distillation)**
- **原理**:知识蒸馏是通过训练一个“小模型”(学生模型)来逼近一个或多个“大模型”(教师模型)的行为,而不是直接融合权重。虽然这并非直接的权重融合,但可以看作是一种权重迁移的方式。
- **步骤**:
- 使用教师模型生成软标签(Soft Targets),学生模型通过匹配这些软标签来学习教师模型的知识。
- 蒸馏过程中,学生模型的权重逐渐逼近教师模型的权重表示。
- **应用场景**:
- 模型压缩:将大模型(如 BERT、GPT 等)蒸馏为较小的模型,适合在资源有限的设备上部署。
- 提高小模型的性能:在不增加复杂度的情况下,提升轻量模型的表现。
### 6. **联邦学习中的聚合方法 (Federated Averaging - FedAvg)**
- **原理**:联邦学习中,多个客户端在本地训练各自的模型,然后将模型权重发送到服务器,服务器通过加权平均的方式生成全局模型。
- **公式**:
$$W_{\text{global}} = \sum_{i=1}^N \frac{n_i}{n} W_i$$
其中, $n_i$ 是第 $i$ 个客户端的样本数量, $n$ 是所有客户端样本数量的总和。
- **应用场景**:
- 联邦学习:用于保护数据隐私的分布式训练方法,数据存留在本地,每个客户端只发送模型权重到服务器进行聚合。
### 7. **最优化方法 (Optimization-based Fusion)**
- **原理**:通过最优化方法找到多个模型权重的最佳组合,最大化某个目标函数(例如交叉熵、精度等)。常见方法包括基于梯度下降的优化。
- **步骤**:
- 定义一个目标函数来度量模型融合后的表现。
- 使用优化算法(如SGD、Adam)迭代更新融合后的权重,直到目标函数收敛。
- **应用场景**:
- 适合在融合时需要考虑模型性能的情境。
- 通常用于复杂模型的组合优化。
### 8. **剪枝后的权重融合 (Pruned Model Fusion)**
- **原理**:首先对模型权重进行剪枝(即移除不重要的权重),然后对剪枝后的模型进行融合。
- **步骤**:
- 先对多个模型进行剪枝,保留重要权重。
- 对保留的权重进行加权平均或其他融合操作。
- **应用场景**:
- 模型压缩:通过剪枝和权重融合相结合,可以大大减少模型的存储和计算量,同时保持性能。
### 9. **弹性融合 (Elastic Weight Consolidation, EWC)**
- **原理**:EWC 是一种用于避免灾难性遗忘(catastrophic forgetting)的技术,尤其是在多任务学习中。它通过计算模型参数的重要性,并对重要参数施加较大的正则化项,来约束模型在新任务上的训练过程中不偏离原有权重太多。
- **公式**:
$$L = L_{\text{new task}} + \frac{\lambda}{2} \sum_i F_i (\theta_i - \theta^*_{i,\text{old task}})^2$$
其中, $F_i$ 是 Fisher 信息矩阵,代表参数 $\theta_i$ 的重要性, $\theta^*_{\text{old task}}$ 是旧任务中的最优权重。
- **应用场景**:
- 多任务学习:特别是连续学习(continual learning)中的权重融合,确保模型在学习新任务时不会遗忘旧任务的知识。
在深度学习模型的训练过程中,优化器起着至关重要的作用。随着模型规模的增大,尤其是在 Transformer 等大型模型中,传统的优化器如 Adam 可能会因为显存占用过大而受到限制。为了解决这个问题,Google 在 2018 年提出了 **Adafactor** 优化器,它在保持性能的同时,大幅降低了显存消耗,特别适用于大规模模型的训练。
Adafactor 优化器通过对二阶矩的近似和自适应学习率的调整,有效地降低了大型模型训练过程中的显存占用,同时保持了模型的性能。
**优势概括**:
- **显存高效**:显著降低显存消耗,支持大规模模型训练。
- **性能优异**:在保持或提升模型性能的同时,减少资源需求。
- **自适应学习率**:简化了超参数调节过程。
## 一、Adafactor提出的背景
### 1. 显存占用问题
- **Adam 优化器**:需要为每个参数维护一阶和二阶矩(即动量和二阶动量),这对于大型模型来说,显著增加了显存消耗。
- **挑战**:在训练大型模型(如 Transformer)时,显存或内存可能成为瓶颈,限制了模型的规模和训练效率。
### 2. 目标
- **降低显存占用**:设计一种优化器,减少参数状态的存储需求。
- **保持性能**:在降低内存的同时,不显著影响模型的收敛速度和最终性能。
## 二、Adafactor 的原理
### 1. 基于 Adam 和 Adagrad
Adafactor 可以被视为对 Adam 和 Adagrad 的改进,结合了两者的优点:
- **Adagrad**:对学习率进行适应性调整,但会累积二阶梯度平方,可能导致学习率过小。
- **Adam**:引入了一阶和二阶动量的指数滑动平均,缓解了 Adagrad 的问题,但需要存储与参数同等大小的一阶和二阶动量。
### 2. 核心思想
- **低秩近似二阶矩**:利用参数矩阵的结构特性,对二阶矩进行低秩分解,从而减少存储需求。
- **分解方法**:对于二维参数矩阵,分别计算行和列的二阶矩,从而避免存储完整的二阶矩。
### 3. 公式推导
#### **假设**
- 参数矩阵 $\mathbf{W}$ 为 $m \times n$ 的矩阵。
- 梯度矩阵为 $\mathbf{G}$ 。
#### **二阶矩估计**
- **传统方法**:需要存储一个 $m \times n$ 的矩阵 $\mathbf{V}$ ,表示梯度的二阶矩估计。
- **Adafactor 方法**:
- **行方向的二阶矩**:
$$\mathbf{r}_t = \text{ReduceMean}(\mathbf{G}_t^2, \text{axis}=1)$$
$\mathbf{r}_t$ 是一个长度为 $m$ 的向量。
- **列方向的二阶矩**:
$$\mathbf{c}_t = \text{ReduceMean}(\mathbf{G}_t^2, \text{axis}=0)$$
$\mathbf{c}_t$ 是一个长度为 $n$ 的向量。
- **二阶矩的近似重构**:
$\mathbf{V}_t \approx \mathbf{r}_t \mathbf{c}_t^\top$
这样只需存储 $\mathbf{r}_t$ 和 $\mathbf{c}_t$ ,而不是完整的 $\mathbf{V}_t$ 。
#### **参数更新**
- **规范化梯度**:
$$\hat{\mathbf{G}}_t = \frac{\mathbf{G}_t}{\sqrt{\mathbf{V}_t} + \epsilon}$$
- **带有学习率的更新**:
$$\mathbf{W}_{t+1} = \mathbf{W}_t - \eta_t \hat{\mathbf{G}}_t$$
其中 $\eta_t$ 是学习率。
### 4. 学习率的自适应调整
Adafactor 提出了对学习率进行自适应调整的方法,以替代外部指定的全局学习率:
$$\eta_t = \eta \cdot \min\left( \frac{1}{\sqrt{t}}, \frac{1}{\sqrt{\mathbf{V}_t}} \right)$$
- **优点**:无需手动设置学习率,优化过程更加稳定。
## 三、Adafactor 的特点
### 1. 显存效率高
- **参数状态存储需求低**:只需存储每个参数矩阵的行和列方向的二阶矩向量。
- **相比 Adam**:Adafactor 将显存占用从 $O(N)$ 降低到 $O(\sqrt{N})$ ,其中 $N$ 是参数数量。
### 2. 适用于大型模型
- **Transformer 等模型**:在大型 Transformer 模型(如神经机器翻译)中,Adafactor 能有效降低内存占用,支持更大的批量训练。
### 3. 保持性能
- **收敛速度和效果**:在许多任务中,Adafactor 的表现与 Adam 相当,甚至在某些情况下更优。
### 4. 自适应学习率
- **无需手动调节**:Adafactor 可以自动调整学习率,减少了调参的工作量。
## 四、与其他优化器的比较
### 1. 与 Adam 的比较
- **内存占用**:
- Adam:需要存储一阶和二阶矩,各 $O(N)$ 。
- Adafactor:二阶矩存储需求降低到 $O(\sqrt{N})$ 。
- **性能**:在大多数情况下,Adafactor 的性能与 Adam 相当。
### 2. 与 Adagrad 的比较
- **学习率衰减**:Adagrad 会导致学习率持续衰减,可能过早停止学习。
- **Adafactor**:通过指数滑动平均和规范化,缓解了学习率过快衰减的问题。
### 3. 与 SGD 的比较
- **收敛速度**:Adafactor 作为自适应优化器,通常比 SGD 收敛更快。
- **稳定性**:自适应调整梯度,训练过程更稳定。
梯度裁剪(Gradient Clipping)是深度学习中一种简单但有效的技术,**用于控制反向传播过程中梯度的大小,避免梯度爆炸问题**。它主要用于确保模型训练的稳定性,特别是在训练深层神经网络或循环神经网络(RNN/LSTM)时,梯度的值可能会急剧增大。梯度裁剪通过限制梯度的大小,防止过大的梯度导致权重更新过度,是提高模型训练稳定性的重要工具。
### 1. **梯度裁剪的背景**
在深度学习模型的训练过程中,尤其是深层网络或循环神经网络中,常见的两个问题是**梯度消失(Gradient Vanishing)**和**梯度爆炸(Gradient Explosion)**。梯度裁剪的引入主要是为了解决梯度爆炸问题。
- **梯度消失**:随着网络层数的增加,反向传播时梯度逐渐减小,导致在靠近输入层的参数几乎没有更新,模型难以学习到有效的表示。
- **梯度爆炸**:与梯度消失相反,梯度爆炸是指梯度在反向传播时迅速增大,尤其在深层网络中,这种现象会导致非常大的权重更新,模型训练过程不稳定,甚至无法收敛。
其中,梯度爆炸问题会导致:
- **训练不稳定**:损失函数剧烈波动,训练过程不稳定。
- **参数发散**:权重更新过度,导致权重值非常大,模型无法收敛,甚至可能出现溢出(NaN 值)。
- **过大的学习步长**:过大的梯度会使得优化器更新时跳跃到远离最优解的位置,导致模型训练失效。
### 2. **什么是梯度裁剪**
梯度裁剪(Gradient Clipping)是一种控制反向传播过程中梯度大小的技术。当梯度的范数超过设定的阈值时,对梯度进行裁剪(缩放),以确保梯度的范数不会过大。这样可以防止梯度爆炸,保持模型训练的稳定性。
梯度裁剪主要有两种常见方式:
- **基于梯度范数的裁剪**(Clipping by Norm):如果梯度的 L2 范数超过设定的阈值,将其缩放到设定的阈值。
- **基于梯度值的裁剪**(Clipping by Value):直接限制每个梯度分量的绝对值在某个区间内。
#### 2.1 **基于梯度范数的裁剪**
这是最常用的梯度裁剪方法。其思想是,如果整个梯度向量的 L2 范数(或者其他范数)超过某个指定的阈值,则将其缩放到该阈值。
假设梯度向量为 $g$ ,其 L2 范数为 $||g||$ ,裁剪操作可以定义为:
$$\text{if} \ ||g|| > \text{max\_grad\_norm} \quad \text{then} \quad g \leftarrow g \times \frac{\text{max\_grad\_norm}}{||g||}$$
其中:
- $g$ 是当前的梯度向量。
- $||g||$ 是梯度的 L2 范数。
- `max_grad_norm` 是我们设定的梯度范数阈值。
- 如果梯度的 L2 范数大于 `max_grad_norm`,则对梯度进行缩放,使其不超过阈值,保持梯度的方向不变。
#### 2.2 **基于梯度值的裁剪**
这种方式是对梯度的每个分量进行裁剪,直接将梯度的每个分量限制在一个区间 $[-v, v]$ 内,具体裁剪规则如下:
$$g_i \leftarrow \min(\max(g_i, -v), v)$$
其中 $g_i$ 是梯度向量中的每个分量, $v$ 是设定的裁剪阈值。这种裁剪方法对每个分量单独处理,但不考虑梯度的整体结构(如向量范数)。
### 3. **梯度裁剪的作用**
梯度裁剪的主要作用是通过限制梯度的大小来防止梯度爆炸,从而保证模型训练的稳定性。它在以下几个场景中特别有用:
#### 3.1 **循环神经网络(RNN)和长短期记忆网络(LSTM)**
RNN 和 LSTM 是顺序处理的模型,它们的梯度在反向传播时需要通过多个时间步累积,因此非常容易出现梯度爆炸和梯度消失的问题。梯度裁剪可以有效地限制每一步的梯度大小,防止梯度爆炸。
#### 3.2 **深度网络**
在非常深的神经网络中,梯度的传播路径较长,梯度爆炸的风险较大。通过裁剪梯度,可以避免训练过程中梯度值过大导致的参数更新不稳定。
#### 3.3 **强化学习**
强化学习中的策略梯度法有时会面临梯度波动较大的问题,特别是当环境中的奖励函数不稳定或有噪声时。梯度裁剪可以平滑梯度的变化,使得模型的学习过程更加稳定。
### 4. **梯度裁剪的实现**
梯度裁剪的实现非常简单,它通常是在计算出梯度后对梯度进行额外的处理,以下是梯度裁剪的常见实现步骤:
1. **反向传播**:首先计算模型参数的梯度。
2. **计算梯度的范数**:计算梯度向量的 L2 范数,或根据其他范数(如 L1 范数)进行计算。
3. **裁剪梯度**:如果梯度的范数超过设定的阈值,将梯度进行缩放,使其范数不超过该阈值。
4. **更新参数**:用裁剪后的梯度更新模型参数。
### 5. **如何选择梯度裁剪的阈值**
选择合适的梯度裁剪阈值是一个实验性的问题,通常需要根据具体任务和模型的行为进行调试。以下是一些经验性建议:
- **默认值**:在大多数情况下,`1.0` 是一个常用的默认阈值,尤其是在 RNN/LSTM 模型中。它能在大多数任务中提供较好的稳定性。
- **梯度波动较大时**:如果发现训练过程中损失函数波动剧烈,或者模型训练不稳定,可以尝试减小阈值(如 0.5 或更小)。
- **模型收敛较慢时**:如果模型在训练时梯度值一直较小,可以尝试增大阈值,以允许梯度有更大的更新步长。
- **动态调整**:在一些高级训练技巧中,可以动态调整梯度裁剪的阈值,例如在训练初期设置较大的阈值以加快收敛速度,而在训练后期减小阈值以稳定优化过程。
### 6. **梯度裁剪的优点与局限性**
#### 6.1 **优点**
- **防止梯度爆炸**:梯度裁剪可以有效避免梯度过大导致的训练不稳定问题,尤其在深层网络和 RNN 中非常有用。
- **训练稳定性**:通过控制梯度的大小,模型的训练过程更加稳定,优化器的步长不会因为梯度过大而过度更新权重。
- **易于实现**:梯度裁剪的实现非常简单,并且已经被各大深度学习框架广泛支持。
#### 6.2 **局限性**
- **不能解决梯度消失问题**:梯度裁剪只能防止梯度爆炸,而对于梯度消失问题没有帮助。要解决梯度消失问题,通常需要采用其他技术(如 LSTM、残差网络等)。
- **影响梯度的自然流动**:过度的梯度裁剪可能会削弱模型的学习能力,尤其是在训练的初期。因为裁剪可能会阻止模型参数做出更大范围的更新,影响优化器找到更优解。
- **需要调优阈值**:梯度裁剪的阈值并不是一成不变的,通常需要根据具体任务、数据集和模型架构进行实验调优。
在AI行业中,**CNN(卷积神经网络)**和**Transformer**结合的架构将 CNN 的局部特征提取能力和 Transformer 的全局特征捕获能力相结合,具备多个显著优势。
## 1. 局部和全局特征的有效结合
- **CNN 提取局部特征**:CNN 通过卷积操作和池化层,擅长从图像中提取局部的空间特征,比如边缘、纹理和形状等。这种局部特征对于视觉任务非常重要,因为它们包含了物体的基本形状信息。
- **Transformer 捕捉全局依赖关系**:Transformer 通过自注意力机制,可以在全局范围内建模任意两个位置之间的依赖关系,因此在捕捉全局上下文信息方面非常强大。
- **结合的优势**:CNN 和 Transformer 的组合能够在捕捉细粒度的局部特征(由 CNN 负责)和理解高层次的全局关系(由 Transformer 负责)之间找到平衡,这使得模型在处理复杂任务时更具优势。
## 2. 计算效率和模型性能的平衡
- **CNN 的计算效率高**:在处理大尺寸输入(如高分辨率图像)时,CNN 可以通过局部感受野高效地进行计算,因此计算成本较低。
- **Transformer 自注意力机制的灵活性**:Transformer 可以通过自注意力机制对图像的不同区域进行关注,特别是对图像中的重要部分施加更多的权重。
- **结合的优势**:在组合架构中,CNN 负责初步提取特征,并将其输入到 Transformer 中以进一步处理。这样可以减少 Transformer 直接处理高维输入的计算负担,提高整体计算效率。
## 3. 提高模型的鲁棒性和泛化能力
- **CNN 在捕捉空间特征方面具有鲁棒性**:CNN 的卷积操作具有平移不变性(translation invariance),可以对图像的平移、缩放等进行一定程度的适应,因此模型在处理不同视角或位置的物体时具备一定的鲁棒性。
- **Transformer 的全局感知能力增强了泛化能力**:Transformer 的全局注意力机制使得模型能够在特征空间上建立更广泛的联系,增强了模型在复杂场景中的泛化能力。
- **结合的优势**:CNN+Transformer 的组合可以让模型在数据变化较大或数据分布复杂的情况下,依然能够捕获重要特征并保持良好的表现。实验表明,这种组合模型在处理高复杂度数据集(如 ImageNet)时,通常优于纯 CNN 模型或纯 Transformer 模型。
## 4. 多模态任务中的优势
- **CNN 和 Transformer 都能处理多模态输入**:CNN 擅长图像特征提取,而 Transformer 已被广泛用于文本、语音和图像的序列化处理,因此这种组合架构在多模态任务中具有显著优势。
- **结合的优势**:在多模态任务(如图像-文本匹配、视觉问答)中,CNN 可以处理图像特征,Transformer 可以同时处理图像和文本信息。这种架构可以轻松处理异构数据,将不同模态的数据融合在一起,以实现跨模态理解和生成。
**Schedule-Free技术**是一种在深度学习模型训练过程中,通过省去预设的学习率调度(schedule)来进行优化的技术。这种方法旨在通过简化超参数调优过程,提升训练的效率和适应性。Schedule-Free技术的原理在于使用自适应调整和动态优化策略,使得模型在训练过程中不再依赖预设的学习率变化曲线,而是通过其他策略来实现稳定收敛。
### Schedule-Free的核心原理
在传统的优化算法中,比如随机梯度下降(SGD)或Adam,学习率调度是训练过程中的一个重要部分。通常,我们会使用余弦衰减、阶梯衰减或指数衰减等策略,按一定规则动态调整学习率,以确保模型在训练的不同阶段有不同的学习率,这有助于模型在开始时快速收敛,在后期更稳定地微调。然而,这种调度策略需要设定特定的超参数和函数形式,且不同任务可能需要不同的学习率调整曲线。
**Schedule-Free优化**则放弃了传统的学习率调度,而是通过以下几种策略来实现类似的效果:
1. **自适应学习率调整**
Schedule-Free技术通过自适应地调整学习率,而非预设一个固定的学习率变化曲线。这可以借助一些自适应优化算法(例如AdaGrad、RMSprop、Adam等)来实现,它们通过对梯度的变化进行分析,动态调整每一轮的学习率。这样,学习率可以随训练过程自动变化,以适应损失函数的不同阶段。
2. **插值更新**
Schedule-Free技术通过引入插值计算来调整每一轮参数更新的幅度。在每次更新中,会将上一次的参数和当前的梯度信息结合起来,通过插值来生成一个新的更新点,这样模型在每一轮中都能自动找到一个更平滑的更新方向,减少学习率的依赖。这种插值的方式通常会减缓更新的步伐,使得模型逐渐收敛。
在每次迭代中,首先计算一个插值点 $y_t$ ,其公式为:
$y_t = (1 - \beta) z_t + \beta x_t$
其中, $z_t$ 是主要的迭代点, $x_t$ 是用于测试或验证损失计算的点, $\beta$ 是插值系数,通常取值在0到1之间。
4. **平均参数更新**
Schedule-Free方法引入了类似动量更新的概念,即使用历史更新的平均值来平滑参数更新。在每次迭代时,将前几次迭代的更新平均化,使得当前的更新不至于过大或过小,这种平滑处理也在一定程度上减小了对学习率的依赖。具体来说,模型每一步的更新都基于前一步的参数和本轮的梯度值的某种加权平均,这种平均可以帮助模型平滑地收敛。
使用插值点 $y_t$ 计算梯度,并更新主要迭代点 $z_t$ :
$z_{t+1} = z_t - \gamma \nabla f(y_t)$
其中, $\gamma$ 是学习率, $\nabla f(y_t)$ 是在 $y_t$ 处计算的损失函数的梯度。
更新用于测试或验证的点 $x_t$ ,其公式为:
$x_{t+1} = \left(1 - \frac{1}{t+1}\right) x_t + \frac{1}{t+1} z_{t+1}$
该步骤相当于对 $z_{t+1}$ 进行加权平均,使 $x_t$ 平滑地跟随 $z_t$ 的变化。
6. **梯度控制**
在Schedule-Free技术中,还引入了一些基于梯度大小的控制机制。比如,如果某一轮的梯度变化过大,可能会引起收敛不稳定,因此可以将这轮的梯度调整为某个固定值,避免对模型造成过大的影响。这样在每一轮中,模型都能保持稳定的收敛速度,减少训练后期对学习率调度的依赖。
### Schedule-Free的优势与特点
1. **减少超参数调优成本**
传统的学习率调度需要设置和调整多个参数,如初始学习率、衰减步数、衰减幅度等。Schedule-Free技术自动调节学习率,使得这些超参数调优的工作量大大减少,适合快速实验和需要灵活配置的项目。
2. **提升训练稳定性**
Schedule-Free方法通过插值、平均更新等策略,平滑了参数更新过程,避免了因学习率变化过快带来的不稳定。这尤其适合复杂模型和大规模数据集,能更快、更稳定地实现收敛。
3. **适应性强**
Schedule-Free技术对不同的数据集和任务具有较强的适应性。由于其不依赖特定的学习率调度曲线,所以在迁移到新任务或数据集时,无需重新设定学习率策略。这在迁移学习或多任务学习中尤为有用。
4. **更符合分布式训练需求**
在分布式深度学习中,Schedule-Free的自适应特性允许模型在不同节点上自由调整学习率,而不需要同步全局的学习率变化,这简化了分布式训练的协调过程。
### Schedule-Free技术的应用场景
Schedule-Free技术特别适合以下场景:
- **长时间训练**:在需要长时间训练的深度学习任务中,Schedule-Free技术可以稳定、自动地调整学习率,不需要在训练后期手动设置新的学习率曲线。
- **快速实验**:对于实验频繁变化、参数需要快速调整的任务,Schedule-Free可以简化模型的调试和参数设置过程,加快模型迭代速度。
- **迁移学习和微调**:在一些迁移学习和微调任务中,原始模型可能不适用固定的学习率变化,Schedule-Free可以帮助模型在新的数据集或任务中快速适应。
- **多分辨率生成模型**:在生成模型(如AIGC)中,生成不同分辨率的图像可能对学习率有不同需求,Schedule-Free可以灵活调整学习率,适应不同分辨率的生成需求。
Layer Normalization 是一种归一化技术,最初由 Geoffrey Hinton 等人提出,用于AIGC、传统深度学习以及自动驾驶中的模型训练,尤其是在序列建模和自然语言处理任务中效果显著。
LayerNorm 的主要作用是通过对特征维度归一化,稳定模型训练过程,减少对 batch size 的依赖,特别适合序列建模、Transformer 等场景。
### **1. LayerNorm 的定义**
LayerNorm 的核心是对输入的一层神经元的**所有特征维度**进行归一化处理,而不是像 BatchNorm 那样对整个 mini-batch 的样本进行归一化。
#### 数学表达:
对于输入 $x \in \mathbb{R}^{T \times F}$ (通常是序列数据,其中 $T$ 是时间步长, $F$ 是特征维度),LayerNorm 对每个时间步的特征维度 $F$ 进行归一化:
$$
\hat{x} = \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}}
$$
其中:
- $\mu = \frac{1}{F} \sum_{i=1}^{F} x_i$ :特征维度的均值。
- $\sigma^2 = \frac{1}{F} \sum_{i=1}^{F} (x_i - \mu)^2$ :特征维度的方差。
- $\epsilon$ :一个小的正值,用于防止分母为零(数值稳定性)。
经过归一化后,再进行线性变换:
$$
y = \gamma \hat{x} + \beta
$$
- $\gamma, \beta$ :可学习的参数(与输入维度 $F$ 相同),用于恢复网络的表达能力。
### **2. LayerNorm 的作用**
#### **2.1. 缓解内部协变量偏移(Internal Covariate Shift)**
在训练过程中,神经网络的每一层输入分布会随着权重更新而变化,导致模型需要不断适应新的分布,影响训练的稳定性。LayerNorm 通过将每一层的输入归一化为零均值和单位方差,有效缓解了这种问题。
#### **2.2. 提高梯度传播的稳定性**
通过归一化,LayerNorm 减少了输入特征的动态范围波动,避免了梯度爆炸或梯度消失的问题,有助于深层神经网络的训练。
#### **2.3. 更适用于序列建模任务**
与 BatchNorm 依赖 mini-batch 的均值和方差不同,LayerNorm 仅依赖于样本内部的特征维度统计量。这使得 LayerNorm 能够适用于 RNN、Transformer 等序列模型,特别是在处理小批量数据或单样本输入时效果突出。
#### **2.4. 减少对 batch size 的依赖**
BatchNorm 在小批量或不规则 batch size 场景中性能会下降,而 LayerNorm 不受 batch size 的影响,能够在单样本推理或小样本学习中表现稳定。
### **3. 应用场景**
1. **Transformer 模型**
- Transformer 中广泛使用 LayerNorm,例如在自注意力机制和前馈网络中对输入进行归一化。
- 通过归一化提升训练稳定性和模型收敛速度。
2. **RNN 和 LSTM**
- LayerNorm 在序列建模(如 NLP 和时间序列任务)中表现优异,适用于 RNN、LSTM 和 GRU 的内部状态归一化。
3. **小批量或单样本训练**
- LayerNorm 不依赖 batch size,因此在小批量或单样本输入任务(如强化学习、对话系统)中效果显著。
### **4. 注意事项**
1. **计算成本**
- LayerNorm 在特征维度上进行归一化,相比 BatchNorm 对大特征维度数据的计算开销更高。
2. **适配任务**
- LayerNorm 更适合序列任务和 NLP 模型;对于卷积网络任务,GroupNorm 或 BatchNorm 可能更高效。
3. **小数据集场景**
- 当 batch size 无法足够大时,LayerNorm 比 BatchNorm 更稳定。
### **一、权重0初始化能否更新?**
**答案是可以更新,但存在严重限制。**
在神经网络中,权重的更新依赖于反向传播计算的梯度。即使权重初始化为0,只要输入数据非零且损失函数对权重的梯度非零,权重仍会更新。例如,对于一个简单的线性层:
$$
y = Wx + b
$$
其中,权重矩阵 **W** 和偏置 **b** 均初始化为0。
#### **更新机制**
1. **梯度计算**:
在反向传播中,权重的梯度依赖于损失函数对输出的导数以及输入值。例如,对于线性层的权重 **W**,其梯度为:
$$\frac{\partial L}{\partial W} = \frac{\partial L}{\partial y} \cdot x^T$$
即使 **W** 初始为0,只要输入 **x** 和损失梯度 **∂L/∂y** 不为0,梯度 **∂L/∂W** 仍然可以计算。
3. **权重更新**:
使用优化器(如SGD、Adam)更新权重:
$$W_{new} = W_{old} - \eta \cdot \frac{\partial L}{\partial W}$$
其中,**η** 是学习率。只要梯度 **∂L/∂W** 不为0,权重 **W** 就会更新。
**但问题在于**:所有神经元因初始权重相同,导致对称性问题,无法学习多样化特征。
### **二、权重0初始化的优势与劣势**
#### **1. 优势**
- **实现简单**:代码实现方便(如`torch.nn.init.zeros_()`),适合教学或快速原型验证。
- **极少数场景适用**:
- **偏置项初始化**:某些情况下偏置(Bias)初始化为0是合理的(如ReLU激活前)。
- **残差连接**:在残差块中,若残差分支最后一层权重初始为0,可确保初始阶段主分支主导输出(如Transformer中的初始化技巧)。
#### **2. 劣势**
- **对称性问题**:
同一层的所有神经元在初始阶段输出相同,导致梯度更新方向一致。网络退化为“单神经元”模型,失去表达能力。
*示例*:若全连接层的两个神经元权重均为0,输入相同数据时,它们的输出和梯度完全一致,最终学习到相同的特征。
- **梯度消失**:
对于某些激活函数(如Sigmoid),输入接近0时梯度接近0.25(饱和区),远小于线性区梯度(如输入=5时梯度≈0.006),导致训练缓慢。
- **局部最优陷阱**:
权重更新方向单一,模型易收敛到次优解。
### **三、通俗示例:合唱团的失败训练**
**场景**:教练需要训练一个合唱团,每位歌手初始音调完全相同(类比权重0初始化)。
- **问题**:
- 所有歌手初始音色一致,无法通过练习(梯度更新)发展出高音、中音、低音的多样性。
- 最终合唱团只能演唱单一音调,无法表现复杂和声。
**解决方法**:
教练让每位歌手从不同音调开始练习(类比随机初始化),才能逐步形成多声部合唱。
### **四、AIGC、传统深度学习以及自动驾驶领域典型应用案例**
#### **1. AIGC(生成式人工智能)**
- **场景**:Stable Diffusion生成高分辨率图像。
- **问题**:若生成器的某些卷积层权重初始为0,模型无法生成多样化的纹理细节(如发丝、云层)。
- **解决方案**:
- 使用He初始化或Xavier初始化,确保权重多样性。
- **例外情况**:在ControlNet等控制模块中,部分层的权重初始为0,以逐步学习外部条件(如边缘检测图)的影响。
#### **2. 传统深度学习**
- **场景**:ResNet50模型进行图像分类。
- **问题**:残差块中若所有卷积层权重初始为0,残差分支失效,模型退化为普通CNN,无法训练深层网络。
- **解决方案**:
- 对残差分支最后一层卷积使用0初始化,确保初始阶段残差输出为0,主分支主导(缓解梯度爆炸)。
- 其他层使用随机初始化(如Kaiming正态分布)。
#### **3. 自动驾驶**
- **场景**:激光雷达点云聚类(如欧氏聚类算法)。
- **问题**:若聚类中心初始化为相同值(类比权重0初始化),无法区分行人与车辆。
- **解决方案**:
- 使用K-means++初始化,选择分散的初始聚类中心。
- **例外情况**:在目标检测模型的最后一层(边界框回归),偏置项可初始为0,表示默认无偏移。
### **五、总结**
- **权重0初始化**在极少数场景下有价值(如残差网络控制初始输出),但绝大多数情况下会导致模型失效。
- **正确初始化策略**(如随机初始化、He初始化)是AI模型成功的基石。
- **不同的行业应用**需结合AIGC、传统深度学习以及自动驾驶领域知识选择初始化方法,平衡训练效率与模型性能。
- [1.有哪些方法能提升CNN模型的泛化能力](#user-content-1有哪些方法能提升cnn模型的泛化能力)
- [2.BN层面试高频问题大汇总](#user-content-2bn层面试高频问题大汇总)
- [3.Instance Normalization的作用](#user-content-3instance-normalization的作用)
- [4.有哪些提高GAN训练稳定性的Tricks](#user-content-4有哪些提高gan训练稳定性的tricks)
- [1.输入Normalize](#user-content-1输入normalize)
- [2.替换原始的GAN损失函数和标签反转](#user-content-2替换原始的gan损失函数和标签反转)
- [3.使用具有球形结构的随机噪声$Z$作为输入](#user-content-3使用具有球形结构的随机噪声z作为输入)
- [4.使用BatchNorm](#user-content-4使用batchnorm)
- [5.避免使用ReLU,MaxPool等操作引入稀疏梯度](#user-content-5避免使用relu,maxpool等操作引入稀疏梯度)
- [6.使用Soft和Noisy的标签](#user-content-6使用soft和noisy的标签)
- [7.使用Adam优化器](#user-content-7使用adam优化器)
- [8.追踪训练失败的信号](#user-content-8追踪训练失败的信号)
- [9.在输入端适当添加噪声](#user-content-9在输入端适当添加噪声)
- [10.生成器和判别器差异化训练](#user-content-10生成器和判别器差异化训练)
- [11.Two Timescale Update Rule (TTUR)](#user-content-11two-timescale-update-rule-ttur)
- [12.Gradient Penalty (梯度惩罚)](#user-content-12gradient-penalty-(梯度惩罚))
- [13.Spectral Normalization(谱归一化)](#user-content-13spectral-normalization(谱归一化))
- [14.使用多个GAN结构](#user-content-14使用多个gan结构)
- [5.什么是超参数?有哪些常用的超参数?](#user-content-5什么是超参数?有哪些常用的超参数?)
- [6.如何寻找到最优超参数?](#user-content-6如何寻找到最优超参数?)
- [7.Spectral Normalization的相关知识](#user-content-7spectral-normalization的相关知识)
- [8.什么是EMA?](#8.什么是EMA?)
- [9.深度学习中有哪些经典的优化器?](#user-content-9深度学习中有哪些经典的优化器?)
- [10.深度学习中常用的学习率衰减策略有哪些?](#user-content-10深度学习中常用的学习率衰减策略有哪些?)
- [11.什么是方向导数?](#user-content-11什么是方向导数?)
- [12.什么是梯度](#user-content-12什么是梯度?)
- [13.为什么沿梯度方向是函数变化最快的方向?](#user-content-13为什么沿梯度方向是函数变化最快的方向?)
- [14.T5LayerNorm和LayerNorm的区别是什么?](#user-content-14T5LayerNorm和LayerNorm的区别是什么?)
- [15.什么是xavier初始化?](#user-content-15什么是xavier初始化?)
- [16.深度学习训练过程中,如果设置的学习率过大,会导致什么问题?](#user-content-16深度学习训练过程中,如果设置的学习率过大,会导致什么问题?)
- [17.介绍一下深度学习中的学习率衰减?](#user-content-17介绍一下深度学习中的学习率衰减?)
- [18.深度学习训练过程中,如果设置的学习率过小,会导致什么问题?](#user-content-18深度学习训练过程中,如果设置的学习率过小,会导致什么问题?)
- [19.深度学习中模型权重融合有哪些主流的方法?](#user-content-19深度学习中模型权重融合有哪些主流的方法?)
- [20.什么是adafactor优化器?](#user-content-20什么是adafactor优化器?)
- [21.什么是深度学习中的梯度裁剪技术?](#user-content-21什么是深度学习中的梯度裁剪技术?)
- [22.CNN+Transformer组合的架构有哪些优势?](#user-content-22CNN+Transformer组合的架构有哪些优势?)
- [23.介绍一下schedule_free优化器的原理](#user-content-23介绍一下schedule_free优化器的原理)
- [24.LayerNorm有什么作用?](#user-content-24LayerNorm有什么作用?)
- [25.AI模型权重0初始化,在训练过程中还能更新权重吗?AI模型权重0初始化有哪些优势和劣势?](#user-content-25AI模型权重0初始化,在训练过程中还能更新权重吗?AI模型权重0初始化有哪些优势和劣势?)
1.有哪些方法能提升CNN模型的泛化能力
1. 采集更多数据:数据决定算法的上限。
2. 优化数据分布:数据类别均衡。
3. 选用合适的目标函数。
4. 设计合适的网络结构。
5. 数据增强。
6. 权值正则化。
7. 使用合适的优化器等。
2.BN层面试高频问题大汇总
BN层解决了什么问题?
统计机器学习中的一个经典假设是“源空间(source domain)和目标空间(target domain)的数据分布(distribution)是一致的”。如果不一致,那么就出现了新的机器学习问题,如transfer learning/domain adaptation等。而covariate shift就是分布不一致假设之下的一个分支问题,它是指源空间和目标空间的条件概率是一致的,但是其边缘概率不同。对于神经网络的各层输出,由于它们经过了层内卷积操作,其分布显然与各层对应的输入信号分布不同,而且差异会随着网络深度增大而增大,但是它们所能代表的label仍然是不变的,这便符合了covariate shift的定义。
因为神经网络在做非线性变换前的激活输入值随着网络深度加深,其分布逐渐发生偏移或者变动(即上述的covariate shift)。之所以训练收敛慢,一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近(比如sigmoid),所以这导致反向传播时低层神经网络的梯度消失,这是训练深层神经网络收敛越来越慢的本质原因。而BN就是通过一定的正则化手段,把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布,避免因为激活函数导致的梯度弥散问题。所以与其说BN的作用是缓解covariate shift,也可以说BN可缓解梯度弥散问题。
BN的公式

其中scale和shift是两个可学的参数,因为减去均值除方差未必是最好的分布。比如数据本身就很不对称,或者激活函数未必是对方差为1的数据有最好的效果。所以要加入缩放及平移变量来完善数据分布以达到比较好的效果。
BN层训练和测试的不同
在训练阶段,BN层是对每个batch的训练数据进行标准化,即用每一批数据的均值和方差。(每一批数据的方差和标准差不同)
而在测试阶段,我们一般只输入一个测试样本,并没有batch的概念。因此这个时候用的均值和方差是整个数据集训练后的均值和方差,可以通过滑动平均法求得:
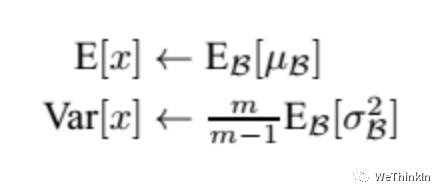
上面式子简单理解就是:对于均值来说直接计算所有batch $u$ 值的平均值;然后对于标准偏差采用每个batch $σ_B$ 的无偏估计。
在测试时,BN使用的公式是:
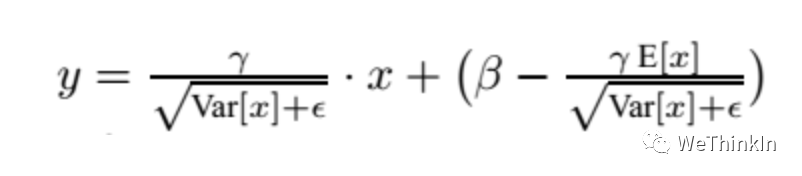
BN训练时为什么不用整个训练集的均值和方差?
因为用整个训练集的均值和方差容易过拟合,对于BN,其实就是对每一batch数据标准化到一个相同的分布,而不同batch数据的均值和方差会有一定的差别,而不是固定的值,这个差别能够增加模型的鲁棒性,也会在一定程度上减少过拟合。
BN层用在哪里?
在CNN中,BN层应该用在非线性激活函数前面。由于神经网络隐藏层的输入是上一层非线性激活函数的输出,在训练初期其分布还在剧烈改变,此时约束其一阶矩和二阶矩无法很好地缓解 Covariate Shift;而BN的分布更接近正态分布,限制其一阶矩和二阶矩能使输入到激活函数的值分布更加稳定。
BN层的参数量
我们知道 $γ$ 和 $β$ 是需要学习的参数,而BN的本质就是利用优化学习改变方差和均值的大小。在CNN中,因为网络的特征是对应到一整张特征图上的,所以做BN的时候也是以特征图为单位而不是按照各个维度。比如在某一层,特征图数量为 $c$ ,那么做BN的参数量为 $c * 2$ 。
BN的优缺点
**优点:**
1. 可以选择较大的初始学习率。因为这个算法收敛很快。
2. 可以不用dropout,L2正则化。
3. 不需要使用局部响应归一化。
4. 可以把数据集彻底打乱。
5. 模型更加健壮。
**缺点:**
1. Batch Normalization非常依赖Batch的大小,当Batch值很小时,计算的均值和方差不稳定。
2. 所以BN不适用于以下几个场景:小Batch,RNN等。
3.Instance Normalization的作用
Instance Normalization(IN)和Batch Normalization(BN)一样,也是Normalization的一种方法,只是IN是作用于单张图片,而BN作用于一个Batch。
BN对Batch中的每一张图片的同一个通道一起进行Normalization操作,而IN是指单张图片的单个通道单独进行Normalization操作。如下图所示,其中C代表通道数,N代表图片数量(Batch)。

IN适用于生成模型中,比如图片风格迁移。因为图片生成的结果主要依赖于某个图像实例,所以对整个Batch进行Normalization操作并不适合图像风格化的任务,在风格迁移中使用IN不仅可以加速模型收敛,并且可以保持每个图像实例之间的独立性。
下面是IN的公式:
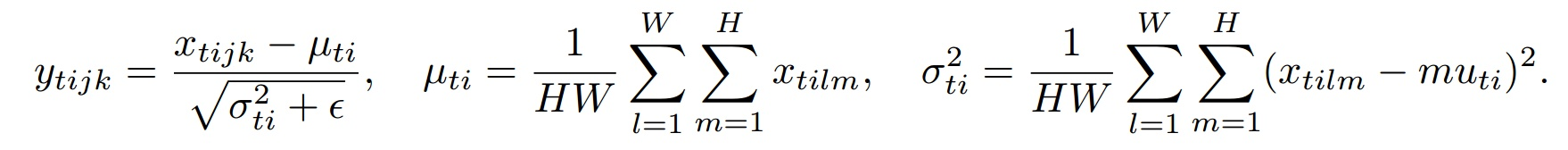
其中t代表图片的index,i代表的是feature map的index。
4.有哪些提高GAN训练稳定性的Tricks
1.输入Normalize
1. 将输入图片Normalize到 $[-1,1]$ 之间。
2. 生成器最后一层的输出使用Tanh激活函数。
Normalize非常重要,没有处理过的图片是没办法收敛的。图片Normalize一种简单的方法是(images-127.5)/127.5,然后送到判别器去训练。同理生成的图片也要经过判别器,即生成器的输出也是-1到1之间,所以使用Tanh激活函数更加合适。
2.替换原始的GAN损失函数和标签反转
1. 原始GAN损失函数会出现训练早期梯度消失和Mode collapse(模型崩溃)问题。可以使用Earth Mover distance(推土机距离)来优化。
2. 实际工程中用反转标签来训练生成器更加方便,即把生成的图片当成real的标签来训练,把真实的图片当成fake来训练。
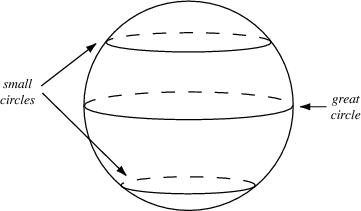
3.使用具有球形结构的随机噪声 $Z$ 作为输入
1. 不要使用均匀分布进行采样

2. 使用高斯分布进行采样

4.使用BatchNorm
1. 一个mini-batch中必须只有real数据或者fake数据,不要把他们混在一起训练。
2. 如果能用BatchNorm就用BatchNorm,如果不能用则用instance normalization。

5.避免使用ReLU,MaxPool等操作引入稀疏梯度
1. GAN的稳定性会因为引入稀疏梯度受到很大影响。
2. 最好使用类LeakyReLU的激活函数。(D和G中都使用)
3. 对于下采样,最好使用:Average Pooling或者卷积+stride。
4. 对于上采样,最好使用:PixelShuffle或者转置卷积+stride。
最好去掉整个Pooling逻辑,因为使用Pooling会损失信息,这对于GAN训练没有益处。
6.使用Soft和Noisy的标签
1. Soft Label,即使用 $[0.7-1.2]$ 和 $[0-0.3]$ 两个区间的随机值来代替正样本和负样本的Hard Label。
2. 可以在训练时对标签加一些噪声,比如随机翻转部分样本的标签。
7.使用Adam优化器
1. Adam优化器对于GAN来说非常有用。
2. 在生成器中使用Adam,在判别器中使用SGD。
8.追踪训练失败的信号
1. 判别器的损失=0说明模型训练失败。
2. 如果生成器的损失稳步下降,说明判别器没有起作用。
9.在输入端适当添加噪声
1. 在判别器的输入中加入一些人工噪声。
2. 在生成器的每层中都加入高斯噪声。
10.生成器和判别器差异化训练
1. 多训练判别器,尤其是加了噪声的时候。
11.Two Timescale Update Rule (TTUR)
对判别器和生成器使用不同的学习速度。使用较低的学习率更新生成器,判别器使用较高的学习率进行更新。
12.Gradient Penalty (梯度惩罚)
使用梯度惩罚机制可以极大增强 GAN 的稳定性,尽可能减少mode collapse问题的产生。
13.Spectral Normalization(谱归一化)
Spectral normalization可以用在判别器的weight normalization技术,可以确保判别器是K-Lipschitz连续的。
14.使用多个GAN结构
可以使用多个GAN/多生成器/多判别器结构来让GAN训练更稳定,提升整体效果,解决更难的问题。
5.什么是超参数?有哪些常用的超参数?
### 什么是超参数?
在深度学习中,**超参数(Hyperparameters)是指在训练开始前设置的模型参数,不是通过训练学习得到的**。超参数的选择对模型性能有很大的影响,不同的超参数设置可能导致显著不同的训练结果。
### 常见的超参数包括:
1. **预处理(Data Augmentation、Normalization and Standardization)**:对输入数据进行预处理。
2. **批量大小(Batch Size)**:每次梯度更新使用的训练样本数量。
3. **学习率(Learning Rate)**:控制模型权重更新的步伐。
4. **学习率衰减(Learning Rate Decay)**:控制学习率随时间逐渐减小的方式。
5. **优化算法/优化器(Optimizer)**:如SGD、Adam、RMSprop等,控制模型权重的更新方式。
6. **损失函数(Loss Function)**:设置训练目标。
8. **迭代次数(Number of Epochs)**:训练过程中遍历整个训练集的次数。
9. **神经网络结构(Network Architecture)**:如层数、每层的神经元数量等。
10. **正则化参数(Regularization Parameters)**:如L2正则化系数、Dropout率等。
11. **激活函数(Activation Function)**:决定每个神经元的输出形式。
12. **权重初始化(Weight Initialization)**:决定模型的初始权重。
6.如何寻找到最优超参数?
**找到最优超参数的过程通常被称为超参数优化(Hyperparameter Optimization)**。常用的方法包括以下几种:
#### 1. **手动调整(Manual Tuning)**:
手动调整超参数是最简单但最费时的方法,通常依赖于经验和试错。可以通过观察模型在验证集上的性能来逐步调整超参数。
#### 2. **网格搜索(Grid Search)**:
网格搜索是一种系统的尝试多个超参数组合的方法。
- **步骤**:
1. 定义每个超参数的可能取值范围。
2. 穷举所有可能的超参数组合。
3. 对每个组合进行交叉验证,评估模型在验证集上的性能。
4. 选择性能最好的组合作为最优超参数。
- **缺点**:计算成本高,特别是超参数数量多和取值范围大的情况下。
#### 3. **随机搜索(Random Search)**:
随机搜索是一种在超参数空间中随机采样进行尝试的方法。
- **步骤**:
1. 定义每个超参数的可能取值范围。
2. 随机采样一定数量的超参数组合。
3. 对每个组合进行交叉验证,评估模型在验证集上的性能。
4. 选择性能最好的组合作为最优超参数。
- **优点**:比网格搜索更有效率,通常在相同计算成本下能找到更好的超参数组合。
#### 4. **贝叶斯优化(Bayesian Optimization)**:
贝叶斯优化是一种利用贝叶斯统计理论的方法,通过构建超参数与模型性能之间的概率模型来选择最优超参数。
- **步骤**:
1. 选择初始点,训练模型并评估性能。
2. 构建代理模型(通常是高斯过程)来模拟超参数空间。
3. 使用代理模型选择下一个最有可能提升性能的超参数组合。
4. 训练模型并更新代理模型。
5. 重复步骤3和4,直到达到预定的迭代次数或时间限制。
- **优点**:比随机搜索和网格搜索更高效,适合高维和复杂的超参数空间。
#### 5. **遗传算法(Genetic Algorithms)**:
遗传算法是一种基于生物进化原理的优化算法。
- **步骤**:
1. 初始化一个包含多个超参数组合的种群。
2. 通过交叉和变异生成新的超参数组合。
3. 根据模型性能评估每个组合的适应度,选择适应度高的组合进行下一代繁衍。
4. 重复步骤2和3,直到达到预定的迭代次数或性能。
- **优点**:能探索复杂的超参数空间,适合解决多峰优化问题。
#### 6. **超参数调优库**:
一些开源的超参数调优库提供了自动化的超参数优化功能。
- **常见库**:
- **Hyperopt**:支持贝叶斯优化,基于TPE(Tree of Parzen Estimators)。
- **Optuna**:灵活且高效的超参数优化库,支持贝叶斯优化、随机搜索和其他自定义优化算法。
- **Ray Tune**:支持多种搜索算法和分布式超参数优化。
- **Scikit-Optimize**:基于Scikit-Learn的优化库,支持贝叶斯优化。
### 示例:使用Optuna进行超参数优化
以下是使用Optuna进行超参数优化的简单示例:
```python
import optuna
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score
# 加载数据集
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=42)
# 定义目标函数
def objective(trial):
# 定义超参数的搜索空间
C = trial.suggest_loguniform('C', 1e-5, 1e2)
gamma = trial.suggest_loguniform('gamma', 1e-5, 1e-1)
# 创建模型
model = SVC(C=C, gamma=gamma)
# 训练模型
model.fit(X_train, y_train)
# 评估模型
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
return accuracy
# 创建Optuna研究对象并进行优化
study = optuna.create_study(direction='maximize')
study.optimize(objective, n_trials=100)
# 输出最优超参数
print('Best trial:')
trial = study.best_trial
print(f' Accuracy: {trial.value}')
print(' Params: ')
for key, value in trial.params.items():
print(f' {key}: {value}')
```
通过这种方法,可以高效地寻找最优超参数组合,从而提升模型性能。
7.Spectral Normalization的相关知识
Spectral Normalization是一种wegiht Normalization技术,和weight-clipping以及gradient penalty一样,也是让模型满足1-Lipschitz条件的方式之一。
Lipschitz(利普希茨)条件限制了函数变化的剧烈程度,即函数的梯度,来确保统计的有界性。因此函数更加平滑,在神经网络的优化过程中,参数变化也会更稳定,不容易出现梯度爆炸。
Lipschitz条件的约束如下所示:
其中 $K$ 代表一个常数,即利普希茨常数。若 $K=1$ ,则是1-Lipschitz。
在GAN领域,Spectral Normalization有很多应用。在WGAN中,只有满足1-Lipschitz约束时,W距离才能转换成较好求解的对偶问题,使得WGAN更加从容的训练。
如果想让矩阵A映射: $R^{n}\to R^{m}$ 满足K-Lipschitz连续,K的最小值为 $\sqrt{\lambda_{1}}$ ( $\lambda_{1}$ 是 $A_TA$ 的最大特征值),那么要想让矩阵A满足1-Lipschitz连续,只需要在A的所有元素上同时除以 $\sqrt{\lambda_{1}}$ (Spectral norm)。
Spectral Normalization实际上在做的事,是将每层的参数矩阵除以自身的最大奇异值,本质上是一个逐层SVD的过程,但是真的去做SVD就太耗时了,所以采用幂迭代的方法求解。过程如下图所示:

得到谱范数 $\sigma_l(W)$ 后,每个参数矩阵上的参数皆除以它,以达到Normalization的目的。
8.什么是EMA?
EMA(指数移动平均,Exponential Moving Average)是一种在深度学习和统计领域常用的技术,特别是在参数优化和数据平滑处理中非常有用。在深度学习中,EMA 常用于模型训练过程中参数的更新,以帮助提高模型的稳定性和性能。
### EMA 的工作原理
EMA 的核心思想是对数据或参数进行加权平均,其中较新的观测值会被赋予更高的权重。这种方法可以快速反映最近的变化,同时还能保留一部分之前的信息,从而在保持数据平滑的同时减少噪声的影响。即将每次梯度更新后的权值和前一次的权重进行联系,使得本次更新收到上次权值的影响。
公式表示为:
$$EMA_t = \alpha \times x_t + (1 - \alpha) \times EMA_{t-1}$$
其中:
- $EMA_t$ 是在时间点 t 的 EMA 值。
- $x_t$ 是在时间点 t 的观测值。
- $\alpha$ 是平滑因子,通常在 0 和 1 之间。
### EMA 在深度学习中的应用
在深度学习中,EMA 可用于模型参数的更新。例如,在训练一个深度神经网络时,通过计算参数的 EMA 可以得到更稳定的模型版本。这在训练过程中尤其有用,因为它可以减少参数更新中的高频波动,从而帮助模型更好地收敛。
### 优势
使用 EMA 更新模型参数的优势包括:
- **减少过拟合**:EMA 可以平滑模型在训练过程中的表现,避免过度追踪训练数据中的噪声。
- **增强泛化能力**:通过平滑化参数更新,模型在未见数据上的表现往往更加稳定和强健。
ema版本的模型可以生成更多创意性的结果,适合训练使用
9.深度学习中有哪些经典的优化器?
### SGD(随机梯度下降)
随机梯度下降的优化算法在科研和工业界是很常用的。
很多理论和工程问题都能转化成对目标函数进行最小化的数学问题。
举个例子:梯度下降(Gradient Descent)就好比一个人想从高山上奔跑到山谷最低点,用最快的方式奔向最低的位置。
SGD的公式:

动量(Momentum)公式:

基本的mini-batch SGD优化算法在深度学习取得很多不错的成绩。然而也存在一些问题需解决:
1. 选择恰当的初始学习率很困难。
2. 学习率调整策略受限于预先指定的调整规则。
3. 相同的学习率被应用于各个参数。
4. 高度非凸的误差函数的优化过程,如何避免陷入大量的局部次优解或鞍点。
### AdaGrad(自适应梯度)
AdaGrad优化算法(Adaptive Gradient,自适应梯度),它能够对每个不同的参数调整不同的学习率,对频繁变化的参数以更小的步长进行更新,而稀疏的参数以更大的步长进行更新。
AdaGrad公式:


$g_{t,i}$ 表示t时刻的 $\theta_{i}$ 梯度。
$G_{t,ii}$ 表示t时刻参数 $\theta_{i}$ 的梯度平方和。
与SGD的核心区别在于计算更新步长时,增加了分母:梯度平方累积和的平方根。此项能够累积各个参数 $\theta_{i}$ 的历史梯度平方,频繁更新的梯度,则累积的分母逐渐偏大,那么更新的步长相对就会变小,而稀疏的梯度,则导致累积的分母项中对应值比较小,那么更新的步长则相对比较大。
AdaGrad能够自动为不同参数适应不同的学习率(平方根的分母项相当于对学习率α进进行了自动调整,然后再乘以本次梯度),大多数的框架实现采用默认学习率α=0.01即可完成比较好的收敛。
**优势:** 在数据分布稀疏的场景,能更好利用稀疏梯度的信息,比标准的SGD算法更有效地收敛。
**缺点:** 主要缺陷来自分母项的对梯度平方不断累积,随时间的增加,分母项越来越大,最终导致学习率收缩到太小无法进行有效更新。
### RMSProp
RMSProp结合梯度平方的指数移动平均数来调节学习率的变化。能够在不稳定的目标函数情况下进行很好地收敛。
计算t时刻的梯度:

计算梯度平方的指数移动平均数(Exponential Moving Average), $\gamma$ 是遗忘因子(或称为指数衰减率),依据经验,默认设置为0.9。

梯度更新的时候,与AdaGrad类似,只是更新的梯度平方的期望(指数移动均值),其中 $\varepsilon = 10^{-8}$ ,避免除数为0。默认学习率 $\alpha = 0.001$ 。

**优势:** 能够克服AdaGrad梯度急剧减小的问题,在很多应用中都展示出优秀的学习率自适应能力。尤其在不稳定(Non-Stationary)的目标函数下,比基本的SGD、Momentum、AdaGrad表现更良好。
### Adam
Adam优化器结合了AdaGrad和RMSProp两种优化算法的优点。对梯度的一阶矩估计(First Moment Estimation,即梯度的均值)和二阶矩估计(Second Moment Estimation,即梯度的未中心化的方差)进行综合考虑,计算出更新步长。
**Adam的优势:**
1. 实现简单,计算高效,对内存需求少。
2. 参数的更新不受梯度的伸缩变换影响。
3. 超参数具有很好的解释性,且通常无需调整或仅需很少的微调。
4. 更新的步长能够被限制在大致的范围内(初始学习率)。
5. 能自然地实现步长退火过程(自动调整学习率)。
6. 很适合应用于大规模的数据及参数的场景。
7. 适用于不稳定目标函数。
8. 适用于梯度稀疏或梯度存在很大噪声的问题。
**Adam的实现原理:**

计算t时刻的梯度:

然后计算梯度的指数移动平均数, $m_{0}$ 初始化为0。
类似于Momentum算法,综合考虑之前累积的梯度动量。
$\beta_{1}$ 系数为指数衰减率,控制动量和当前梯度的权重分配,通常取接近于1的值。默认为0.9。

接着,计算梯度平方的指数移动平均数, $v_{0}$ 初始化为0。
$\beta_{2}$ 系数为指数衰减率,控制之前的梯度平方的影响情况。默认为0.999。
类似于RMSProp算法,对梯度平方进行加权均值。

由于 $m_{0}$ 初始化为0,会导致$m_{t}$偏向于0,尤其在训练初期阶段。
所以,此处需要对梯度均值$m_{t}$进行偏差纠正,降低偏差对训练初期的影响。

同时 $v_{0}$ 也要进行偏差纠正:

最后总的公式如下所示:

其中默认学习率 $\alpha = 0.001$ , $\varepsilon = 10^{-8}$ 避免除数变为0。
从表达式中可以看出,对更新的步长计算,能够从梯度均值和梯度平方两个角度进行自适应地调节,而不是直接由当前梯度决定。
**Adam的不足:**
虽然Adam算法目前成为主流的优化算法,不过在很多领域里(如计算机视觉的图像识别、NLP中的机器翻译)的最佳成果仍然是使用带动量(Momentum)的SGD来获取到的。
10.深度学习中常用的学习率衰减策略有哪些?
在AI领域中,合适的学习率调整策略对于模型的训练效果和收敛速度至关重要。
学习率衰减(或调整)是用来在训练过程中逐步减小学习率的方法,目的是帮助模型更好地收敛,避免训练过程中的振荡或不稳定。
以下是几种常用的学习率衰减方法:
### 1. 固定学习率衰减
这是最简单的衰减方法之一,其中学习率按预定的固定间隔和固定因子进行减少。例如,每过10个epoch将学习率乘以0.1。
### 2. 指数衰减
在指数衰减模式下,学习率按照指数函数逐步减小,通常定义为:
$\text{Learning Rate} = \text{Initial Learning Rate} \times e^{-\text{decay rate} \times \text{epoch}}$
其中,decay rate是一个预先设定的常数,epoch是当前的训练轮数。
### 3. 时间基衰减
时间基衰减与指数衰减类似,但学习率的衰减与训练的具体时间(通常是epoch数)更直接相关:
$\text{Learning Rate} = \frac{\text{Initial Learning Rate}}{1 + \text{decay rate} \times \text{epoch}}$
### 4. 阶梯衰减
在阶梯衰减中,学习率在一系列预设的epoch(如每20个epoch)后显著下降。这种衰减通常是手动设置的,非常直观,允许模型在较高的学习率下快速学习,并在训练后期通过较低的学习率细化模型。
### 5. 余弦衰减
余弦衰减是一种较新的策略,它模仿了余弦函数的形状来调整学习率,从初始学习率逐渐减小到接近零的值。这种方法在一些周期性或重启的训练策略中特别有效,可以帮助模型跳出局部最小值。
### 6. 适应性学习率方法
这包括像Adam和RMSprop这样的优化算法,这些算法本身就能够调整每个参数的学习率,通常基于历史梯度的平方(用于归一化梯度)。这些方法自动调整学习率,无需显式的衰减策略。
### 7. 热身和重启
- **学习率热身**:在训练初期,学习率从一个较低的值逐渐增加到设定的初始学习率。这有助于模型在训练初期稳定下来,防止初始学习率过高导致的不稳定。
- **周期性重启**:学习率按周期性地增加和减少,每次“重启”都从较高的学习率开始,然后再次衰减。这种方法有助于模型跳出局部最小值,寻找更好的全局最小值。
这些学习率调整方法可以单独使用,也可以结合使用,以达到最佳的训练效果。选择哪种衰减策略取决于具体任务、模型的复杂性以及训练数据的特点。在实际应用中,通常需要通过多次实验来确定最合适的学习率调整策略。
11.什么是方向导数
- 导数是二维平面中,曲线上某一点沿着x轴方向变化的速率
- 偏导数是在三维空间中,曲面上某一点沿着x轴方向或y轴方向变化的速率
- 方向导数是在三维空间中,曲面上某一点沿着任一方向的变化率
定理:如果函数 $f(x,y)$ 在点 $P_{0}\left(x_{0}, y_{0}\right)$ 可微分,那么函数在该点沿任一方向 $l$ 的方向导数存在,且有
$$\frac{\partial f}{\partial \vec{l}}=\frac{\partial f}{\partial x} \cdot \cos \alpha+\frac{\partial f}{\partial y} \cdot \cos \beta$其中$\vec{l}=\{\cos \alpha, \cos \beta\}$$
12.什么是梯度
设函数 $z=f(x,y)$ 在平面区域$D$内具有一阶连续偏导数,对于区域$D$中的每一个点都可以确定一个向量 $f_{x}(x, y) \vec{i}+f_{y}(x, y) \vec{j}$ 成为函数在该点的梯度,记为:
$$\text{gradf}(\mathrm{x}, \mathrm{y})=\nabla f(x, y)= \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} = f_{x}(x, y) \vec{i}+f_{y}(x, y) \vec{j}$$
13.为什么沿梯度方向是函数变化最快的方向?
梯度下降法,是机器学习、深度学习中比较核心也是较为常用的优化算法,但为什么沿梯度方向,函数变化最快?方向导数与梯度有什么关系?
设 $\vec{e}=\{\cos \alpha, \cos \beta\}$ 是方向 $l$ 上的单位向量,则
$$\frac{\partial f}{\partial \vec{l}}=\frac{\partial f}{\partial x} \cdot \cos \alpha+\frac{\partial f}{\partial y} \cdot \cos \beta = \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} {\cos \alpha, \cos \beta\}=\text{grad} f(x, y) \cdot \vec{e}$$
$=|\text{gradf}(x, y)|\cdot\cos\theta$ ,其中 $\theta$ 为 $\text{gradf}(\mathrm{x}, \mathrm{y})$ 与 $\vec{e}$ 的夹角
1. 当 $\theta =0$ 时,即 $\vec{e}$ 沿着梯度方向,方向导数取得最大值
2. 当 $\theta = \pi/2$ 时,方向导数为0
3. 当 $\theta =\pi$ 时,即 $\vec{e}$ 沿着梯度反方向,方向导数取得最小值
## 综上
当方向导数大于0时,方向导数的大小用来描述函数上升的速率快慢,方向导数越大,表明函数上升越快,当方向导数小于0时,方向导数的大小用来描述函数下降的速率快慢,方向导数越小,表明函数下降越快,即 $\vec{e}$ 沿着梯度反方向,方向导数取得最小值,此时函数下降速率最快。
14.T5LayerNorm和LayerNorm的区别是什么?
比起标准的层归一化(Layer Normalization),T5LayerNorm主要特点是只对网络的权重参数进行缩放(scale),而不进行偏移(shift)。T5LayerNorm的主要公式如下:
$$\text{T5LayerNorm}(x) = \frac{x}{\sqrt{\text{Var}(x) + \epsilon}} \times \text{weight}$$
- $x$ 是输入的张量。
- $\text{Var}(x)$ 是 $x$ 的方差,计算方式是对每个元素平方后求平均值。
- $\epsilon$ 是一个小常数,用于防止除零错误,确保数值稳定性。
- $\text{weight}$ 是一个可训练的参数,用来缩放输出。
总的来说,T5LayerNorm的关键在于:
1. **只进行缩放,不进行偏移**:它不像LayerNorm那样先减去均值再缩放,它只根据输入数据的方差进行缩放。
2. **处理方式简洁但有效**:通过对输入数据的平方均值进行归一化,T5LayerNorm保持了简洁性,并且这种归一化方式在处理较高维度的输入时非常高效。
3. **适应高维数据**:T5LayerNorm特别适用于AIGC大模型中的高维数据输入,因为它能够在保持数值稳定性的同时,减少不必要的计算量。
正是上述的这些特点使得T5LayerNorm成为AI视频大模型中非常实用的归一化方法。
15.什么是xavier初始化?
Xavier初始化(也称为Glorot初始化)是深度学习中用于神经网络权重初始化的一种方法,它在训练深层神经网络时非常重要,尤其是为了避免梯度消失或梯度爆炸问题。Xavier初始化通过设置权重,使得网络层的输入和输出的方差保持一致,从而稳定梯度的传播。
在深度神经网络中,如果权重初始化得不当,随着网络的层数增加,可能会出现梯度消失(vanishing gradient)和梯度爆炸(exploding gradient)的问题。
### 1. Xavier 初始化的原理
Xavier初始化的核心思想是保持网络中的输入和输出的方差相等,以此来稳定梯度的传播。它假设激活函数是线性的,且每一层的输入和输出分布应该保持相似。
具体来说,设某一层有 $n_{\text{in}}$ 个输入神经元和 $n_{\text{out}}$ 个输出神经元,Xavier 初始化会将权重 $W$ 初始化为满足以下分布:
- **均匀分布**:权重从一个均匀分布中采样,其范围为:
$$W \sim \mathcal{U}\left(-\frac{1}{\sqrt{n_{\text{in}}}}, \frac{1}{\sqrt{n_{\text{in}}}}\right)$$
- **正态分布**:权重从一个均值为 0,标准差为 $\frac{1}{\sqrt{n_{\text{in}}}}$ 的正态分布中采样:
$$W \sim \mathcal{N}\left(0, \frac{1}{n_{\text{in}}}\right)$$
这种初始化方式保证了前向传播和反向传播时,梯度不会因为层数增加而出现消失或爆炸的情况。
### 2. Xavier 初始化的推导
在 Xavier 初始化中,目标是保持每一层输出的方差与输入的方差大致相同。假设:
- 输入 $x$ 的方差为 $\text{Var}(x) = \sigma_x^2$
- 权重 $W$ 的方差为 $\text{Var}(W) = \sigma_W^2$
在前向传播时,假设每层的输入 $x$ 具有 $n_{\text{in}}$ 个神经元,权重矩阵为 $W$ ,那么输出 $y$ 的方差应该满足以下条件:
$$\text{Var}(y) = n_{\text{in}} \cdot \text{Var}(W) \cdot \text{Var}(x)$$
为了防止参数权重的方差在传递过程中不断增大或减小,Xavier初始化的目标是让输出方差等于输入方差,即 $\text{Var}(y) = \text{Var}(x)$ 。这样可以推导出权重初始化的条件:
$$n_{\text{in}} \cdot \sigma_W^2 = 1 \quad \Rightarrow \quad \sigma_W^2 = \frac{1}{n_{\text{in}}}$$
这解释了 Xavier 初始化为什么将权重的方差设置为 $\frac{1}{n_{\text{in}}}$ 。
### 3. Xavier 初始化的适用范围
Xavier 初始化适合用于激活函数是对称且线性或接近线性的情况,例如:
- **线性激活函数**
- **双曲正切函数(tanh)**
然而,当激活函数是 ReLU 或其变体(如 Leaky ReLU)时,由于这些激活函数的非线性性质,Xavier 初始化可能不太合适。这时,通常使用 **He 初始化**,它是 Xavier 初始化的变体,专门针对 ReLU 激活函数做了调整。
### 4. Xavier 初始化的改进:He 初始化
对于非对称的激活函数(例如 ReLU),Xavier 初始化的假设可能不再成立。He 初始化专门为这些激活函数设计,公式类似于 Xavier,但调整了方差的计算:
$$W \sim \mathcal{N}(0, \frac{2}{n_{\text{in}}})$$
这种初始化方式能更好地保持梯度在深层网络中的传播。
16.深度学习训练过程中,如果设置的学习率过大,会导致什么问题?
训练过程不稳定:
当学习率过大时,会致使权重更新幅度偏大,进而使损失函数的值在每次迭代中出现剧烈起伏。如此一来,模型参数可能持续在损失函数的不同区域间跳动,引发训练过程的不稳定性,甚至可能出现发散状况。
无法收敛:
由于每次更新的步幅过大,模型或许永远无法抵达或靠近全局最优点或局部最优点。损失函数的值难以稳定在一个较低区间内,模型性能无法提升,训练也就无法实现收敛。
梯度爆炸:
采用较大学习率时,可能引发梯度爆炸问题。梯度值会变得极大,导致参数更新量极为庞大。这不但使训练变得极为艰难,还可能让参数达到极端数值,进一步加重训练的不稳定性。
性能不佳:
即便模型勉强实现收敛,最终得到的模型性能通常也不尽如人意。这是因为参数在损失函数表面跳跃幅度过大,无法精细地调整至最优解附近,致使模型的泛化能力较弱,表现不理想。
17.介绍一下深度学习中的学习率衰减?
学习率衰减(learning rate decay)是深度学习模型训练过程中常用的技术,用于在训练过程中逐渐减小学习率,以帮助模型更好地收敛。常见的学习率衰减方式包括:
时间衰减(Time-based decay):按照固定的周期(epoch)或迭代次数(iteration)减小学习率。例如,每10个epoch将学习率减小一半。
指数衰减(Exponential decay):按照指数函数减小学习率。例如,每10个epoch将学习率减小为原来的0.1倍。
余弦衰减(Cosine decay):按照余弦函数减小学习率。余弦衰减在训练初期可以快速减小学习率,在训练后期可以逐渐减小学习率,有助于模型更好地收敛。
阶梯衰减(Step decay):在预定义的轮次列表处调整学习率。例如,在10、20、30个epoch后将学习率减小为原来的0.1倍。
余弦退火(Cosine annealing):余弦退火是一种特殊的余弦衰减策略,它会在训练过程中逐渐减小学习率,并在训练结束时将学习率减小到0。
学习率预热(Learning rate warmup):学习率预热是指在训练初期使用较小的学习率,随着训练的进行逐渐增大学习率。这种方法可以避免模型在训练初期由于学习率过大而发散。
学习率调整(Learning rate scheduling):根据模型的性能指标(如验证集上的损失)动态调整学习率。常见的调整策略包括学习率退火(learning rate annealing)和学习率周期调整(learning rate cycling)。
学习率优化算法(Learning rate optimizers):一些优化算法(如Adam、RMSprop等)内部包含学习率调整机制,可以在训练过程中自动调整学习率。
选择哪种学习率衰减方式取决于具体任务、模型和数据集的特点。在实际应用中,通常需要通过实验来确定最佳的学习率衰减策略。
18.深度学习训练过程中,如果设置的学习率过小,会导致什么问题?
学习率衰减过早可能引发以下几种状况:
学习率衰减过早可能带来以下情况:
一、训练进程变缓
学习率过早衰减会使模型参数更新的幅度减小,每次迭代中的权重调整变小。这会致使模型在全局最优解附近的搜索速度极为缓慢,从而大幅增加训练时间。
二、易陷局部最优
过早衰减学习率会让模型参数更新步伐变小,这样一来模型更容易被困在局部最优处,难以跳出局部最优去探寻全局最优解。原因在于较小的学习率降低了模型在损失函数表面进行大幅度搜索的能力。
三、未充分利用高学习率阶段
训练初期,较高的学习率能助力模型快速收敛以找到较优解。若学习率过早衰减,模型就无法充分发挥初始高学习率阶段的快速收敛特性,可能致使模型训练效率降低,甚至无法达到理想的初始收敛效果。
四、训练不充分
在训练早期,模型参数处于快速调整阶段。此时若学习率过早衰减,模型可能无法充分训练至较好状态,最终导致模型性能欠佳。因为早期的参数更新需要较大幅度的调整来适应复杂的损失表面结构,而过早衰减的学习率会限制这种能力。
19.深度学习中模型权重融合有哪些主流的方法?
在深度学习中,模型权重融合(Model Weight Fusion)是指将多个模型的参数(权重)进行合并或融合,旨在**提高模型的性能或实现模型压缩**。权重融合的方法在模型集成、知识蒸馏、联邦学习等场景中具有广泛应用。以下是一些主流的权重融合方法:
### 1. **简单加权平均法 (Simple Weight Averaging)**
- **原理**:通过对多个模型的权重取加权平均,生成一个融合后的新模型。
- **公式**:
$$W_{\text{fused}} = \frac{1}{N} \sum_{i=1}^N W_i$$
其中, $W_i$ 是第 $i$ 个模型的权重, $N$ 是模型的数量。
- **应用场景**:
- 联邦学习(Federated Learning):每个客户端训练本地模型,服务器通过聚合客户端模型权重来更新全局模型。
- 模型集成:结合多个相似结构的模型来生成更具鲁棒性的模型。
### 2. **线性插值法 (Linear Interpolation)**
- **原理**:给定两个模型,通过在它们的权重空间中进行线性插值生成新的模型。
- **公式**:
$$W_{\text{fused}} = \alpha W_1 + (1 - \alpha) W_2$$
其中, $W_1$ 和 $W_2$ 是两个模型的权重, $\alpha$ 是插值系数,通常取值在 $[0,1]$ 之间。
- **应用场景**:
- 在优化模型时,用于平衡两个模型之间的性能表现,特别是在权重空间中寻找局部最优解。
### 3. **逐层融合 (Layer-wise Fusion)**
- **原理**:通过逐层将多个模型的权重进行融合,而不是全局地直接对所有权重进行加权平均。
- **步骤**:
- 对应层的权重矩阵或张量进行加权平均或其他操作。
- 每层都可以使用不同的融合方法。
- **应用场景**:
- 在具有相同架构的模型之间融合时效果较好。
- 常用于知识蒸馏或模型压缩,逐层传递知识。
### 4. **基于权重相似性的融合 (Weight Similarity-based Fusion)**
- **原理**:基于多个模型的权重相似性来确定融合方式。通过计算不同模型权重的距离,调整不同模型的权重融合比例。
- **常用方法**:
- 计算每个层权重的余弦相似性(Cosine Similarity)或欧氏距离(Euclidean Distance),来确定如何调整每个模型的权重贡献。
- **应用场景**:
- 当模型结构相似但参数值差异较大时,利用权重相似性可以更智能地融合模型。
- 特别适用于使用不同数据集或不同初始化训练得到的模型。
### 5. **知识蒸馏 (Knowledge Distillation)**
- **原理**:知识蒸馏是通过训练一个“小模型”(学生模型)来逼近一个或多个“大模型”(教师模型)的行为,而不是直接融合权重。虽然这并非直接的权重融合,但可以看作是一种权重迁移的方式。
- **步骤**:
- 使用教师模型生成软标签(Soft Targets),学生模型通过匹配这些软标签来学习教师模型的知识。
- 蒸馏过程中,学生模型的权重逐渐逼近教师模型的权重表示。
- **应用场景**:
- 模型压缩:将大模型(如 BERT、GPT 等)蒸馏为较小的模型,适合在资源有限的设备上部署。
- 提高小模型的性能:在不增加复杂度的情况下,提升轻量模型的表现。
### 6. **联邦学习中的聚合方法 (Federated Averaging - FedAvg)**
- **原理**:联邦学习中,多个客户端在本地训练各自的模型,然后将模型权重发送到服务器,服务器通过加权平均的方式生成全局模型。
- **公式**:
$$W_{\text{global}} = \sum_{i=1}^N \frac{n_i}{n} W_i$$
其中, $n_i$ 是第 $i$ 个客户端的样本数量, $n$ 是所有客户端样本数量的总和。
- **应用场景**:
- 联邦学习:用于保护数据隐私的分布式训练方法,数据存留在本地,每个客户端只发送模型权重到服务器进行聚合。
### 7. **最优化方法 (Optimization-based Fusion)**
- **原理**:通过最优化方法找到多个模型权重的最佳组合,最大化某个目标函数(例如交叉熵、精度等)。常见方法包括基于梯度下降的优化。
- **步骤**:
- 定义一个目标函数来度量模型融合后的表现。
- 使用优化算法(如SGD、Adam)迭代更新融合后的权重,直到目标函数收敛。
- **应用场景**:
- 适合在融合时需要考虑模型性能的情境。
- 通常用于复杂模型的组合优化。
### 8. **剪枝后的权重融合 (Pruned Model Fusion)**
- **原理**:首先对模型权重进行剪枝(即移除不重要的权重),然后对剪枝后的模型进行融合。
- **步骤**:
- 先对多个模型进行剪枝,保留重要权重。
- 对保留的权重进行加权平均或其他融合操作。
- **应用场景**:
- 模型压缩:通过剪枝和权重融合相结合,可以大大减少模型的存储和计算量,同时保持性能。
### 9. **弹性融合 (Elastic Weight Consolidation, EWC)**
- **原理**:EWC 是一种用于避免灾难性遗忘(catastrophic forgetting)的技术,尤其是在多任务学习中。它通过计算模型参数的重要性,并对重要参数施加较大的正则化项,来约束模型在新任务上的训练过程中不偏离原有权重太多。
- **公式**:
$$L = L_{\text{new task}} + \frac{\lambda}{2} \sum_i F_i (\theta_i - \theta^*_{i,\text{old task}})^2$$
其中, $F_i$ 是 Fisher 信息矩阵,代表参数 $\theta_i$ 的重要性, $\theta^*_{\text{old task}}$ 是旧任务中的最优权重。
- **应用场景**:
- 多任务学习:特别是连续学习(continual learning)中的权重融合,确保模型在学习新任务时不会遗忘旧任务的知识。
20.什么是adafactor优化器?
在深度学习模型的训练过程中,优化器起着至关重要的作用。随着模型规模的增大,尤其是在 Transformer 等大型模型中,传统的优化器如 Adam 可能会因为显存占用过大而受到限制。为了解决这个问题,Google 在 2018 年提出了 **Adafactor** 优化器,它在保持性能的同时,大幅降低了显存消耗,特别适用于大规模模型的训练。
Adafactor 优化器通过对二阶矩的近似和自适应学习率的调整,有效地降低了大型模型训练过程中的显存占用,同时保持了模型的性能。
**优势概括**:
- **显存高效**:显著降低显存消耗,支持大规模模型训练。
- **性能优异**:在保持或提升模型性能的同时,减少资源需求。
- **自适应学习率**:简化了超参数调节过程。
## 一、Adafactor提出的背景
### 1. 显存占用问题
- **Adam 优化器**:需要为每个参数维护一阶和二阶矩(即动量和二阶动量),这对于大型模型来说,显著增加了显存消耗。
- **挑战**:在训练大型模型(如 Transformer)时,显存或内存可能成为瓶颈,限制了模型的规模和训练效率。
### 2. 目标
- **降低显存占用**:设计一种优化器,减少参数状态的存储需求。
- **保持性能**:在降低内存的同时,不显著影响模型的收敛速度和最终性能。
## 二、Adafactor 的原理
### 1. 基于 Adam 和 Adagrad
Adafactor 可以被视为对 Adam 和 Adagrad 的改进,结合了两者的优点:
- **Adagrad**:对学习率进行适应性调整,但会累积二阶梯度平方,可能导致学习率过小。
- **Adam**:引入了一阶和二阶动量的指数滑动平均,缓解了 Adagrad 的问题,但需要存储与参数同等大小的一阶和二阶动量。
### 2. 核心思想
- **低秩近似二阶矩**:利用参数矩阵的结构特性,对二阶矩进行低秩分解,从而减少存储需求。
- **分解方法**:对于二维参数矩阵,分别计算行和列的二阶矩,从而避免存储完整的二阶矩。
### 3. 公式推导
#### **假设**
- 参数矩阵 $\mathbf{W}$ 为 $m \times n$ 的矩阵。
- 梯度矩阵为 $\mathbf{G}$ 。
#### **二阶矩估计**
- **传统方法**:需要存储一个 $m \times n$ 的矩阵 $\mathbf{V}$ ,表示梯度的二阶矩估计。
- **Adafactor 方法**:
- **行方向的二阶矩**:
$$\mathbf{r}_t = \text{ReduceMean}(\mathbf{G}_t^2, \text{axis}=1)$$
$\mathbf{r}_t$ 是一个长度为 $m$ 的向量。
- **列方向的二阶矩**:
$$\mathbf{c}_t = \text{ReduceMean}(\mathbf{G}_t^2, \text{axis}=0)$$
$\mathbf{c}_t$ 是一个长度为 $n$ 的向量。
- **二阶矩的近似重构**:
$\mathbf{V}_t \approx \mathbf{r}_t \mathbf{c}_t^\top$
这样只需存储 $\mathbf{r}_t$ 和 $\mathbf{c}_t$ ,而不是完整的 $\mathbf{V}_t$ 。
#### **参数更新**
- **规范化梯度**:
$$\hat{\mathbf{G}}_t = \frac{\mathbf{G}_t}{\sqrt{\mathbf{V}_t} + \epsilon}$$
- **带有学习率的更新**:
$$\mathbf{W}_{t+1} = \mathbf{W}_t - \eta_t \hat{\mathbf{G}}_t$$
其中 $\eta_t$ 是学习率。
### 4. 学习率的自适应调整
Adafactor 提出了对学习率进行自适应调整的方法,以替代外部指定的全局学习率:
$$\eta_t = \eta \cdot \min\left( \frac{1}{\sqrt{t}}, \frac{1}{\sqrt{\mathbf{V}_t}} \right)$$
- **优点**:无需手动设置学习率,优化过程更加稳定。
## 三、Adafactor 的特点
### 1. 显存效率高
- **参数状态存储需求低**:只需存储每个参数矩阵的行和列方向的二阶矩向量。
- **相比 Adam**:Adafactor 将显存占用从 $O(N)$ 降低到 $O(\sqrt{N})$ ,其中 $N$ 是参数数量。
### 2. 适用于大型模型
- **Transformer 等模型**:在大型 Transformer 模型(如神经机器翻译)中,Adafactor 能有效降低内存占用,支持更大的批量训练。
### 3. 保持性能
- **收敛速度和效果**:在许多任务中,Adafactor 的表现与 Adam 相当,甚至在某些情况下更优。
### 4. 自适应学习率
- **无需手动调节**:Adafactor 可以自动调整学习率,减少了调参的工作量。
## 四、与其他优化器的比较
### 1. 与 Adam 的比较
- **内存占用**:
- Adam:需要存储一阶和二阶矩,各 $O(N)$ 。
- Adafactor:二阶矩存储需求降低到 $O(\sqrt{N})$ 。
- **性能**:在大多数情况下,Adafactor 的性能与 Adam 相当。
### 2. 与 Adagrad 的比较
- **学习率衰减**:Adagrad 会导致学习率持续衰减,可能过早停止学习。
- **Adafactor**:通过指数滑动平均和规范化,缓解了学习率过快衰减的问题。
### 3. 与 SGD 的比较
- **收敛速度**:Adafactor 作为自适应优化器,通常比 SGD 收敛更快。
- **稳定性**:自适应调整梯度,训练过程更稳定。
21.什么是深度学习中的梯度裁剪技术?
梯度裁剪(Gradient Clipping)是深度学习中一种简单但有效的技术,**用于控制反向传播过程中梯度的大小,避免梯度爆炸问题**。它主要用于确保模型训练的稳定性,特别是在训练深层神经网络或循环神经网络(RNN/LSTM)时,梯度的值可能会急剧增大。梯度裁剪通过限制梯度的大小,防止过大的梯度导致权重更新过度,是提高模型训练稳定性的重要工具。
### 1. **梯度裁剪的背景**
在深度学习模型的训练过程中,尤其是深层网络或循环神经网络中,常见的两个问题是**梯度消失(Gradient Vanishing)**和**梯度爆炸(Gradient Explosion)**。梯度裁剪的引入主要是为了解决梯度爆炸问题。
- **梯度消失**:随着网络层数的增加,反向传播时梯度逐渐减小,导致在靠近输入层的参数几乎没有更新,模型难以学习到有效的表示。
- **梯度爆炸**:与梯度消失相反,梯度爆炸是指梯度在反向传播时迅速增大,尤其在深层网络中,这种现象会导致非常大的权重更新,模型训练过程不稳定,甚至无法收敛。
其中,梯度爆炸问题会导致:
- **训练不稳定**:损失函数剧烈波动,训练过程不稳定。
- **参数发散**:权重更新过度,导致权重值非常大,模型无法收敛,甚至可能出现溢出(NaN 值)。
- **过大的学习步长**:过大的梯度会使得优化器更新时跳跃到远离最优解的位置,导致模型训练失效。
### 2. **什么是梯度裁剪**
梯度裁剪(Gradient Clipping)是一种控制反向传播过程中梯度大小的技术。当梯度的范数超过设定的阈值时,对梯度进行裁剪(缩放),以确保梯度的范数不会过大。这样可以防止梯度爆炸,保持模型训练的稳定性。
梯度裁剪主要有两种常见方式:
- **基于梯度范数的裁剪**(Clipping by Norm):如果梯度的 L2 范数超过设定的阈值,将其缩放到设定的阈值。
- **基于梯度值的裁剪**(Clipping by Value):直接限制每个梯度分量的绝对值在某个区间内。
#### 2.1 **基于梯度范数的裁剪**
这是最常用的梯度裁剪方法。其思想是,如果整个梯度向量的 L2 范数(或者其他范数)超过某个指定的阈值,则将其缩放到该阈值。
假设梯度向量为 $g$ ,其 L2 范数为 $||g||$ ,裁剪操作可以定义为:
$$\text{if} \ ||g|| > \text{max\_grad\_norm} \quad \text{then} \quad g \leftarrow g \times \frac{\text{max\_grad\_norm}}{||g||}$$
其中:
- $g$ 是当前的梯度向量。
- $||g||$ 是梯度的 L2 范数。
- `max_grad_norm` 是我们设定的梯度范数阈值。
- 如果梯度的 L2 范数大于 `max_grad_norm`,则对梯度进行缩放,使其不超过阈值,保持梯度的方向不变。
#### 2.2 **基于梯度值的裁剪**
这种方式是对梯度的每个分量进行裁剪,直接将梯度的每个分量限制在一个区间 $[-v, v]$ 内,具体裁剪规则如下:
$$g_i \leftarrow \min(\max(g_i, -v), v)$$
其中 $g_i$ 是梯度向量中的每个分量, $v$ 是设定的裁剪阈值。这种裁剪方法对每个分量单独处理,但不考虑梯度的整体结构(如向量范数)。
### 3. **梯度裁剪的作用**
梯度裁剪的主要作用是通过限制梯度的大小来防止梯度爆炸,从而保证模型训练的稳定性。它在以下几个场景中特别有用:
#### 3.1 **循环神经网络(RNN)和长短期记忆网络(LSTM)**
RNN 和 LSTM 是顺序处理的模型,它们的梯度在反向传播时需要通过多个时间步累积,因此非常容易出现梯度爆炸和梯度消失的问题。梯度裁剪可以有效地限制每一步的梯度大小,防止梯度爆炸。
#### 3.2 **深度网络**
在非常深的神经网络中,梯度的传播路径较长,梯度爆炸的风险较大。通过裁剪梯度,可以避免训练过程中梯度值过大导致的参数更新不稳定。
#### 3.3 **强化学习**
强化学习中的策略梯度法有时会面临梯度波动较大的问题,特别是当环境中的奖励函数不稳定或有噪声时。梯度裁剪可以平滑梯度的变化,使得模型的学习过程更加稳定。
### 4. **梯度裁剪的实现**
梯度裁剪的实现非常简单,它通常是在计算出梯度后对梯度进行额外的处理,以下是梯度裁剪的常见实现步骤:
1. **反向传播**:首先计算模型参数的梯度。
2. **计算梯度的范数**:计算梯度向量的 L2 范数,或根据其他范数(如 L1 范数)进行计算。
3. **裁剪梯度**:如果梯度的范数超过设定的阈值,将梯度进行缩放,使其范数不超过该阈值。
4. **更新参数**:用裁剪后的梯度更新模型参数。
### 5. **如何选择梯度裁剪的阈值**
选择合适的梯度裁剪阈值是一个实验性的问题,通常需要根据具体任务和模型的行为进行调试。以下是一些经验性建议:
- **默认值**:在大多数情况下,`1.0` 是一个常用的默认阈值,尤其是在 RNN/LSTM 模型中。它能在大多数任务中提供较好的稳定性。
- **梯度波动较大时**:如果发现训练过程中损失函数波动剧烈,或者模型训练不稳定,可以尝试减小阈值(如 0.5 或更小)。
- **模型收敛较慢时**:如果模型在训练时梯度值一直较小,可以尝试增大阈值,以允许梯度有更大的更新步长。
- **动态调整**:在一些高级训练技巧中,可以动态调整梯度裁剪的阈值,例如在训练初期设置较大的阈值以加快收敛速度,而在训练后期减小阈值以稳定优化过程。
### 6. **梯度裁剪的优点与局限性**
#### 6.1 **优点**
- **防止梯度爆炸**:梯度裁剪可以有效避免梯度过大导致的训练不稳定问题,尤其在深层网络和 RNN 中非常有用。
- **训练稳定性**:通过控制梯度的大小,模型的训练过程更加稳定,优化器的步长不会因为梯度过大而过度更新权重。
- **易于实现**:梯度裁剪的实现非常简单,并且已经被各大深度学习框架广泛支持。
#### 6.2 **局限性**
- **不能解决梯度消失问题**:梯度裁剪只能防止梯度爆炸,而对于梯度消失问题没有帮助。要解决梯度消失问题,通常需要采用其他技术(如 LSTM、残差网络等)。
- **影响梯度的自然流动**:过度的梯度裁剪可能会削弱模型的学习能力,尤其是在训练的初期。因为裁剪可能会阻止模型参数做出更大范围的更新,影响优化器找到更优解。
- **需要调优阈值**:梯度裁剪的阈值并不是一成不变的,通常需要根据具体任务、数据集和模型架构进行实验调优。
22.CNN+Transformer组合的架构有哪些优势?
在AI行业中,**CNN(卷积神经网络)**和**Transformer**结合的架构将 CNN 的局部特征提取能力和 Transformer 的全局特征捕获能力相结合,具备多个显著优势。
## 1. 局部和全局特征的有效结合
- **CNN 提取局部特征**:CNN 通过卷积操作和池化层,擅长从图像中提取局部的空间特征,比如边缘、纹理和形状等。这种局部特征对于视觉任务非常重要,因为它们包含了物体的基本形状信息。
- **Transformer 捕捉全局依赖关系**:Transformer 通过自注意力机制,可以在全局范围内建模任意两个位置之间的依赖关系,因此在捕捉全局上下文信息方面非常强大。
- **结合的优势**:CNN 和 Transformer 的组合能够在捕捉细粒度的局部特征(由 CNN 负责)和理解高层次的全局关系(由 Transformer 负责)之间找到平衡,这使得模型在处理复杂任务时更具优势。
## 2. 计算效率和模型性能的平衡
- **CNN 的计算效率高**:在处理大尺寸输入(如高分辨率图像)时,CNN 可以通过局部感受野高效地进行计算,因此计算成本较低。
- **Transformer 自注意力机制的灵活性**:Transformer 可以通过自注意力机制对图像的不同区域进行关注,特别是对图像中的重要部分施加更多的权重。
- **结合的优势**:在组合架构中,CNN 负责初步提取特征,并将其输入到 Transformer 中以进一步处理。这样可以减少 Transformer 直接处理高维输入的计算负担,提高整体计算效率。
## 3. 提高模型的鲁棒性和泛化能力
- **CNN 在捕捉空间特征方面具有鲁棒性**:CNN 的卷积操作具有平移不变性(translation invariance),可以对图像的平移、缩放等进行一定程度的适应,因此模型在处理不同视角或位置的物体时具备一定的鲁棒性。
- **Transformer 的全局感知能力增强了泛化能力**:Transformer 的全局注意力机制使得模型能够在特征空间上建立更广泛的联系,增强了模型在复杂场景中的泛化能力。
- **结合的优势**:CNN+Transformer 的组合可以让模型在数据变化较大或数据分布复杂的情况下,依然能够捕获重要特征并保持良好的表现。实验表明,这种组合模型在处理高复杂度数据集(如 ImageNet)时,通常优于纯 CNN 模型或纯 Transformer 模型。
## 4. 多模态任务中的优势
- **CNN 和 Transformer 都能处理多模态输入**:CNN 擅长图像特征提取,而 Transformer 已被广泛用于文本、语音和图像的序列化处理,因此这种组合架构在多模态任务中具有显著优势。
- **结合的优势**:在多模态任务(如图像-文本匹配、视觉问答)中,CNN 可以处理图像特征,Transformer 可以同时处理图像和文本信息。这种架构可以轻松处理异构数据,将不同模态的数据融合在一起,以实现跨模态理解和生成。
23.介绍一下schedule_free优化器的原理
**Schedule-Free技术**是一种在深度学习模型训练过程中,通过省去预设的学习率调度(schedule)来进行优化的技术。这种方法旨在通过简化超参数调优过程,提升训练的效率和适应性。Schedule-Free技术的原理在于使用自适应调整和动态优化策略,使得模型在训练过程中不再依赖预设的学习率变化曲线,而是通过其他策略来实现稳定收敛。
### Schedule-Free的核心原理
在传统的优化算法中,比如随机梯度下降(SGD)或Adam,学习率调度是训练过程中的一个重要部分。通常,我们会使用余弦衰减、阶梯衰减或指数衰减等策略,按一定规则动态调整学习率,以确保模型在训练的不同阶段有不同的学习率,这有助于模型在开始时快速收敛,在后期更稳定地微调。然而,这种调度策略需要设定特定的超参数和函数形式,且不同任务可能需要不同的学习率调整曲线。
**Schedule-Free优化**则放弃了传统的学习率调度,而是通过以下几种策略来实现类似的效果:
1. **自适应学习率调整**
Schedule-Free技术通过自适应地调整学习率,而非预设一个固定的学习率变化曲线。这可以借助一些自适应优化算法(例如AdaGrad、RMSprop、Adam等)来实现,它们通过对梯度的变化进行分析,动态调整每一轮的学习率。这样,学习率可以随训练过程自动变化,以适应损失函数的不同阶段。
2. **插值更新**
Schedule-Free技术通过引入插值计算来调整每一轮参数更新的幅度。在每次更新中,会将上一次的参数和当前的梯度信息结合起来,通过插值来生成一个新的更新点,这样模型在每一轮中都能自动找到一个更平滑的更新方向,减少学习率的依赖。这种插值的方式通常会减缓更新的步伐,使得模型逐渐收敛。
在每次迭代中,首先计算一个插值点 $y_t$ ,其公式为:
$y_t = (1 - \beta) z_t + \beta x_t$
其中, $z_t$ 是主要的迭代点, $x_t$ 是用于测试或验证损失计算的点, $\beta$ 是插值系数,通常取值在0到1之间。
4. **平均参数更新**
Schedule-Free方法引入了类似动量更新的概念,即使用历史更新的平均值来平滑参数更新。在每次迭代时,将前几次迭代的更新平均化,使得当前的更新不至于过大或过小,这种平滑处理也在一定程度上减小了对学习率的依赖。具体来说,模型每一步的更新都基于前一步的参数和本轮的梯度值的某种加权平均,这种平均可以帮助模型平滑地收敛。
使用插值点 $y_t$ 计算梯度,并更新主要迭代点 $z_t$ :
$z_{t+1} = z_t - \gamma \nabla f(y_t)$
其中, $\gamma$ 是学习率, $\nabla f(y_t)$ 是在 $y_t$ 处计算的损失函数的梯度。
更新用于测试或验证的点 $x_t$ ,其公式为:
$x_{t+1} = \left(1 - \frac{1}{t+1}\right) x_t + \frac{1}{t+1} z_{t+1}$
该步骤相当于对 $z_{t+1}$ 进行加权平均,使 $x_t$ 平滑地跟随 $z_t$ 的变化。
6. **梯度控制**
在Schedule-Free技术中,还引入了一些基于梯度大小的控制机制。比如,如果某一轮的梯度变化过大,可能会引起收敛不稳定,因此可以将这轮的梯度调整为某个固定值,避免对模型造成过大的影响。这样在每一轮中,模型都能保持稳定的收敛速度,减少训练后期对学习率调度的依赖。
### Schedule-Free的优势与特点
1. **减少超参数调优成本**
传统的学习率调度需要设置和调整多个参数,如初始学习率、衰减步数、衰减幅度等。Schedule-Free技术自动调节学习率,使得这些超参数调优的工作量大大减少,适合快速实验和需要灵活配置的项目。
2. **提升训练稳定性**
Schedule-Free方法通过插值、平均更新等策略,平滑了参数更新过程,避免了因学习率变化过快带来的不稳定。这尤其适合复杂模型和大规模数据集,能更快、更稳定地实现收敛。
3. **适应性强**
Schedule-Free技术对不同的数据集和任务具有较强的适应性。由于其不依赖特定的学习率调度曲线,所以在迁移到新任务或数据集时,无需重新设定学习率策略。这在迁移学习或多任务学习中尤为有用。
4. **更符合分布式训练需求**
在分布式深度学习中,Schedule-Free的自适应特性允许模型在不同节点上自由调整学习率,而不需要同步全局的学习率变化,这简化了分布式训练的协调过程。
### Schedule-Free技术的应用场景
Schedule-Free技术特别适合以下场景:
- **长时间训练**:在需要长时间训练的深度学习任务中,Schedule-Free技术可以稳定、自动地调整学习率,不需要在训练后期手动设置新的学习率曲线。
- **快速实验**:对于实验频繁变化、参数需要快速调整的任务,Schedule-Free可以简化模型的调试和参数设置过程,加快模型迭代速度。
- **迁移学习和微调**:在一些迁移学习和微调任务中,原始模型可能不适用固定的学习率变化,Schedule-Free可以帮助模型在新的数据集或任务中快速适应。
- **多分辨率生成模型**:在生成模型(如AIGC)中,生成不同分辨率的图像可能对学习率有不同需求,Schedule-Free可以灵活调整学习率,适应不同分辨率的生成需求。
24.LayerNorm有什么作用?
Layer Normalization 是一种归一化技术,最初由 Geoffrey Hinton 等人提出,用于AIGC、传统深度学习以及自动驾驶中的模型训练,尤其是在序列建模和自然语言处理任务中效果显著。
LayerNorm 的主要作用是通过对特征维度归一化,稳定模型训练过程,减少对 batch size 的依赖,特别适合序列建模、Transformer 等场景。
### **1. LayerNorm 的定义**
LayerNorm 的核心是对输入的一层神经元的**所有特征维度**进行归一化处理,而不是像 BatchNorm 那样对整个 mini-batch 的样本进行归一化。
#### 数学表达:
对于输入 $x \in \mathbb{R}^{T \times F}$ (通常是序列数据,其中 $T$ 是时间步长, $F$ 是特征维度),LayerNorm 对每个时间步的特征维度 $F$ 进行归一化:
$$
\hat{x} = \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}}
$$
其中:
- $\mu = \frac{1}{F} \sum_{i=1}^{F} x_i$ :特征维度的均值。
- $\sigma^2 = \frac{1}{F} \sum_{i=1}^{F} (x_i - \mu)^2$ :特征维度的方差。
- $\epsilon$ :一个小的正值,用于防止分母为零(数值稳定性)。
经过归一化后,再进行线性变换:
$$
y = \gamma \hat{x} + \beta
$$
- $\gamma, \beta$ :可学习的参数(与输入维度 $F$ 相同),用于恢复网络的表达能力。
### **2. LayerNorm 的作用**
#### **2.1. 缓解内部协变量偏移(Internal Covariate Shift)**
在训练过程中,神经网络的每一层输入分布会随着权重更新而变化,导致模型需要不断适应新的分布,影响训练的稳定性。LayerNorm 通过将每一层的输入归一化为零均值和单位方差,有效缓解了这种问题。
#### **2.2. 提高梯度传播的稳定性**
通过归一化,LayerNorm 减少了输入特征的动态范围波动,避免了梯度爆炸或梯度消失的问题,有助于深层神经网络的训练。
#### **2.3. 更适用于序列建模任务**
与 BatchNorm 依赖 mini-batch 的均值和方差不同,LayerNorm 仅依赖于样本内部的特征维度统计量。这使得 LayerNorm 能够适用于 RNN、Transformer 等序列模型,特别是在处理小批量数据或单样本输入时效果突出。
#### **2.4. 减少对 batch size 的依赖**
BatchNorm 在小批量或不规则 batch size 场景中性能会下降,而 LayerNorm 不受 batch size 的影响,能够在单样本推理或小样本学习中表现稳定。
### **3. 应用场景**
1. **Transformer 模型**
- Transformer 中广泛使用 LayerNorm,例如在自注意力机制和前馈网络中对输入进行归一化。
- 通过归一化提升训练稳定性和模型收敛速度。
2. **RNN 和 LSTM**
- LayerNorm 在序列建模(如 NLP 和时间序列任务)中表现优异,适用于 RNN、LSTM 和 GRU 的内部状态归一化。
3. **小批量或单样本训练**
- LayerNorm 不依赖 batch size,因此在小批量或单样本输入任务(如强化学习、对话系统)中效果显著。
### **4. 注意事项**
1. **计算成本**
- LayerNorm 在特征维度上进行归一化,相比 BatchNorm 对大特征维度数据的计算开销更高。
2. **适配任务**
- LayerNorm 更适合序列任务和 NLP 模型;对于卷积网络任务,GroupNorm 或 BatchNorm 可能更高效。
3. **小数据集场景**
- 当 batch size 无法足够大时,LayerNorm 比 BatchNorm 更稳定。
25.AI模型权重0初始化,在训练过程中还能更新权重吗?AI模型权重0初始化有哪些优势和劣势?
### **一、权重0初始化能否更新?**
**答案是可以更新,但存在严重限制。**
在神经网络中,权重的更新依赖于反向传播计算的梯度。即使权重初始化为0,只要输入数据非零且损失函数对权重的梯度非零,权重仍会更新。例如,对于一个简单的线性层:
$$
y = Wx + b
$$
其中,权重矩阵 **W** 和偏置 **b** 均初始化为0。
#### **更新机制**
1. **梯度计算**:
在反向传播中,权重的梯度依赖于损失函数对输出的导数以及输入值。例如,对于线性层的权重 **W**,其梯度为:
$$\frac{\partial L}{\partial W} = \frac{\partial L}{\partial y} \cdot x^T$$
即使 **W** 初始为0,只要输入 **x** 和损失梯度 **∂L/∂y** 不为0,梯度 **∂L/∂W** 仍然可以计算。
3. **权重更新**:
使用优化器(如SGD、Adam)更新权重:
$$W_{new} = W_{old} - \eta \cdot \frac{\partial L}{\partial W}$$
其中,**η** 是学习率。只要梯度 **∂L/∂W** 不为0,权重 **W** 就会更新。
**但问题在于**:所有神经元因初始权重相同,导致对称性问题,无法学习多样化特征。
### **二、权重0初始化的优势与劣势**
#### **1. 优势**
- **实现简单**:代码实现方便(如`torch.nn.init.zeros_()`),适合教学或快速原型验证。
- **极少数场景适用**:
- **偏置项初始化**:某些情况下偏置(Bias)初始化为0是合理的(如ReLU激活前)。
- **残差连接**:在残差块中,若残差分支最后一层权重初始为0,可确保初始阶段主分支主导输出(如Transformer中的初始化技巧)。
#### **2. 劣势**
- **对称性问题**:
同一层的所有神经元在初始阶段输出相同,导致梯度更新方向一致。网络退化为“单神经元”模型,失去表达能力。
*示例*:若全连接层的两个神经元权重均为0,输入相同数据时,它们的输出和梯度完全一致,最终学习到相同的特征。
- **梯度消失**:
对于某些激活函数(如Sigmoid),输入接近0时梯度接近0.25(饱和区),远小于线性区梯度(如输入=5时梯度≈0.006),导致训练缓慢。
- **局部最优陷阱**:
权重更新方向单一,模型易收敛到次优解。
### **三、通俗示例:合唱团的失败训练**
**场景**:教练需要训练一个合唱团,每位歌手初始音调完全相同(类比权重0初始化)。
- **问题**:
- 所有歌手初始音色一致,无法通过练习(梯度更新)发展出高音、中音、低音的多样性。
- 最终合唱团只能演唱单一音调,无法表现复杂和声。
**解决方法**:
教练让每位歌手从不同音调开始练习(类比随机初始化),才能逐步形成多声部合唱。
### **四、AIGC、传统深度学习以及自动驾驶领域典型应用案例**
#### **1. AIGC(生成式人工智能)**
- **场景**:Stable Diffusion生成高分辨率图像。
- **问题**:若生成器的某些卷积层权重初始为0,模型无法生成多样化的纹理细节(如发丝、云层)。
- **解决方案**:
- 使用He初始化或Xavier初始化,确保权重多样性。
- **例外情况**:在ControlNet等控制模块中,部分层的权重初始为0,以逐步学习外部条件(如边缘检测图)的影响。
#### **2. 传统深度学习**
- **场景**:ResNet50模型进行图像分类。
- **问题**:残差块中若所有卷积层权重初始为0,残差分支失效,模型退化为普通CNN,无法训练深层网络。
- **解决方案**:
- 对残差分支最后一层卷积使用0初始化,确保初始阶段残差输出为0,主分支主导(缓解梯度爆炸)。
- 其他层使用随机初始化(如Kaiming正态分布)。
#### **3. 自动驾驶**
- **场景**:激光雷达点云聚类(如欧氏聚类算法)。
- **问题**:若聚类中心初始化为相同值(类比权重0初始化),无法区分行人与车辆。
- **解决方案**:
- 使用K-means++初始化,选择分散的初始聚类中心。
- **例外情况**:在目标检测模型的最后一层(边界框回归),偏置项可初始为0,表示默认无偏移。
### **五、总结**
- **权重0初始化**在极少数场景下有价值(如残差网络控制初始输出),但绝大多数情况下会导致模型失效。
- **正确初始化策略**(如随机初始化、He初始化)是AI模型成功的基石。
- **不同的行业应用**需结合AIGC、传统深度学习以及自动驾驶领域知识选择初始化方法,平衡训练效率与模型性能。
点赞
回复
X