文件名称:
激活函数层知识点.md
所在目录:
深度学习基础
文件大小:
16.69 KB
下载地址:
文本预览:
# 目录
- [1.激活函数的作用,常用的激活函数有哪些](#user-content-1激活函数的作用,常用的激活函数有哪些)
- [2.什么是GELU激活函数?](#user-content-2什么是GELU激活函数?)
- [3.什么是SiLU激活函数?](#user-content-3什么是SiLU激活函数?)
- [4.什么是NewGELU激活函数?](#user-content-4什么是NewGELU激活函数?)
- [5.介绍一下 GeLU 计算公式?](#user-content-5.介绍一下GeLU计算公式?)
- [6.介绍一下 Swish 计算公式?](#user-content-6.介绍一下Swish计算公式?)
### 激活函数的作用
激活函数可以引入非线性因素,提升网络的学习表达能力。
### 常用的激活函数
**Sigmoid 激活函数**
函数的定义为:
$$f(x) = \frac{1}{1 + e^{-x}}$$
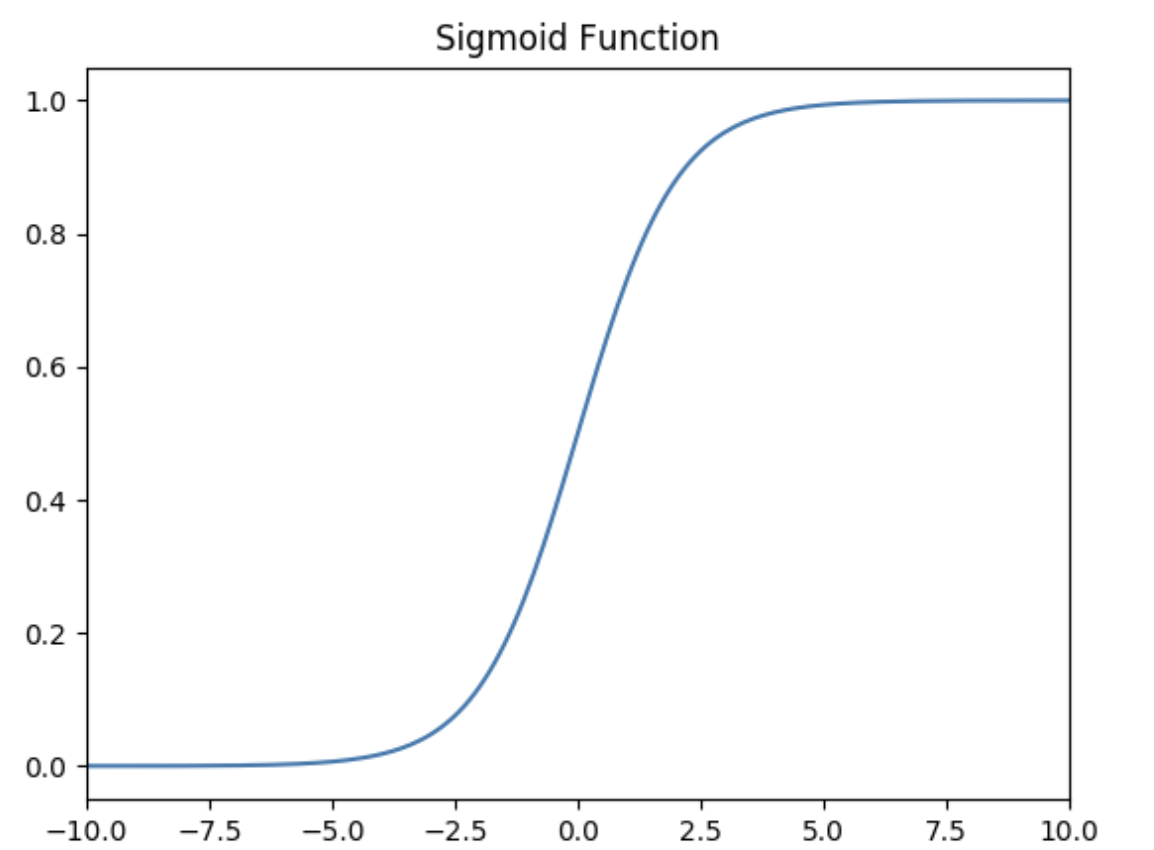
如下图所示,其值域为 $(0,1)$ 。也就是说,输入的每个神经元、节点都会被缩放到一个介于 $0$ 和 $1$ 之间的值。
当 $x$ 大于零时输出结果会趋近于 $1$ ,而当 $x$ 小于零时,输出结果趋向于 $0$ ,由于函数的特性,经常被用作二分类的输出端激活函数。
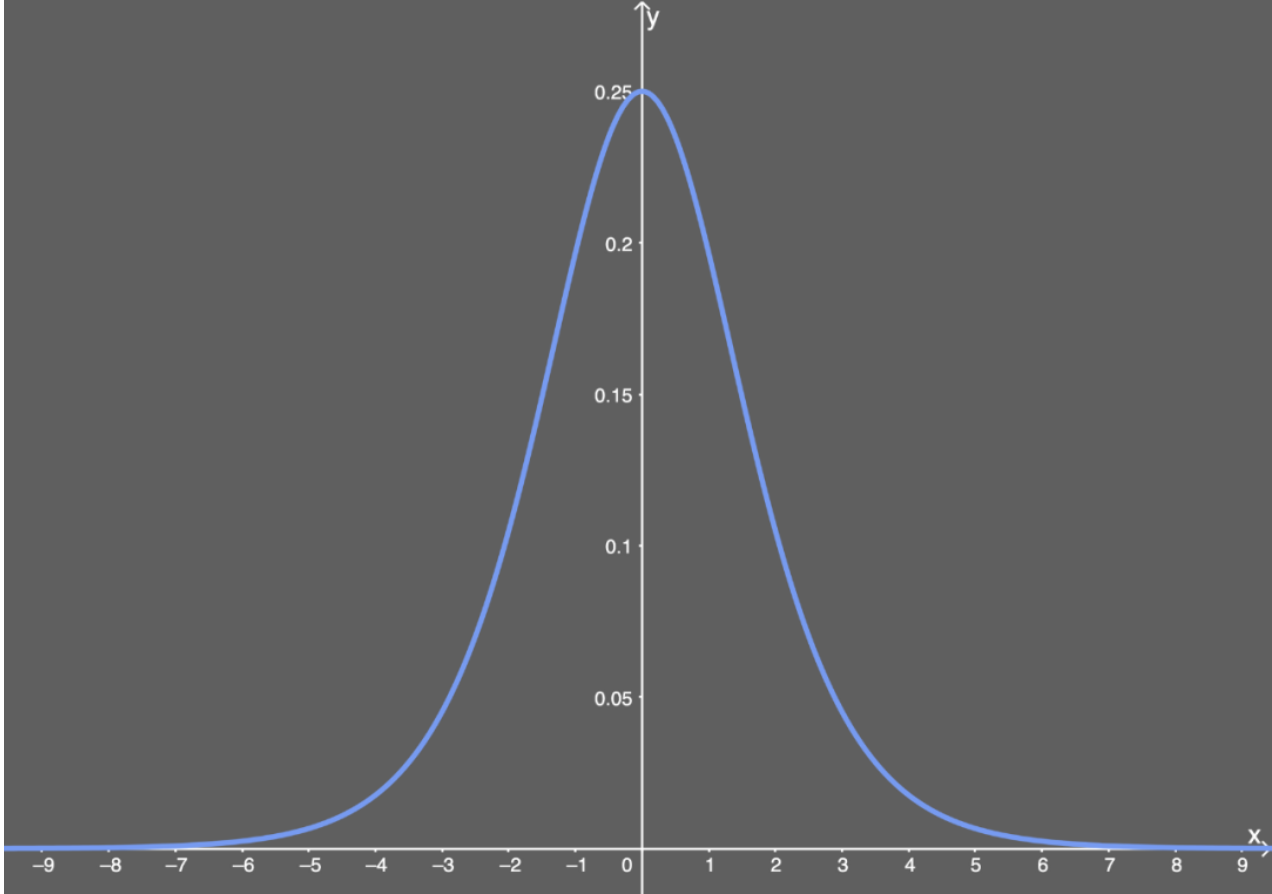
Sigmoid的导数:
$$f^{'}(x)=(\frac{1}{1+e^{-x}})^{'}=\frac{1}{1+e^{-x}}\left( 1- \frac{1}{1+e^{-x}} \right)=f(x)(1-f(x))$$
当 $x=0$ 时, $f(x)'=0.25$ 。
Sigmoid的优点:
1. 平滑
2. 易于求导
3. 可以作为概率,辅助解释模型的输出结果
Sigmoid的缺陷:
1. 当输入数据很大或者很小时,函数的梯度几乎接近于0,这对神经网络在反向传播中的学习非常不利。
2. Sigmoid函数的均值不是0,这使得神经网络的训练过程中只会产生全正或全负的反馈。
3. 导数值恒小于1,反向传播易导致梯度消失。
**Tanh激活函数**
Tanh函数的定义为:
$$f(x) = Tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$$
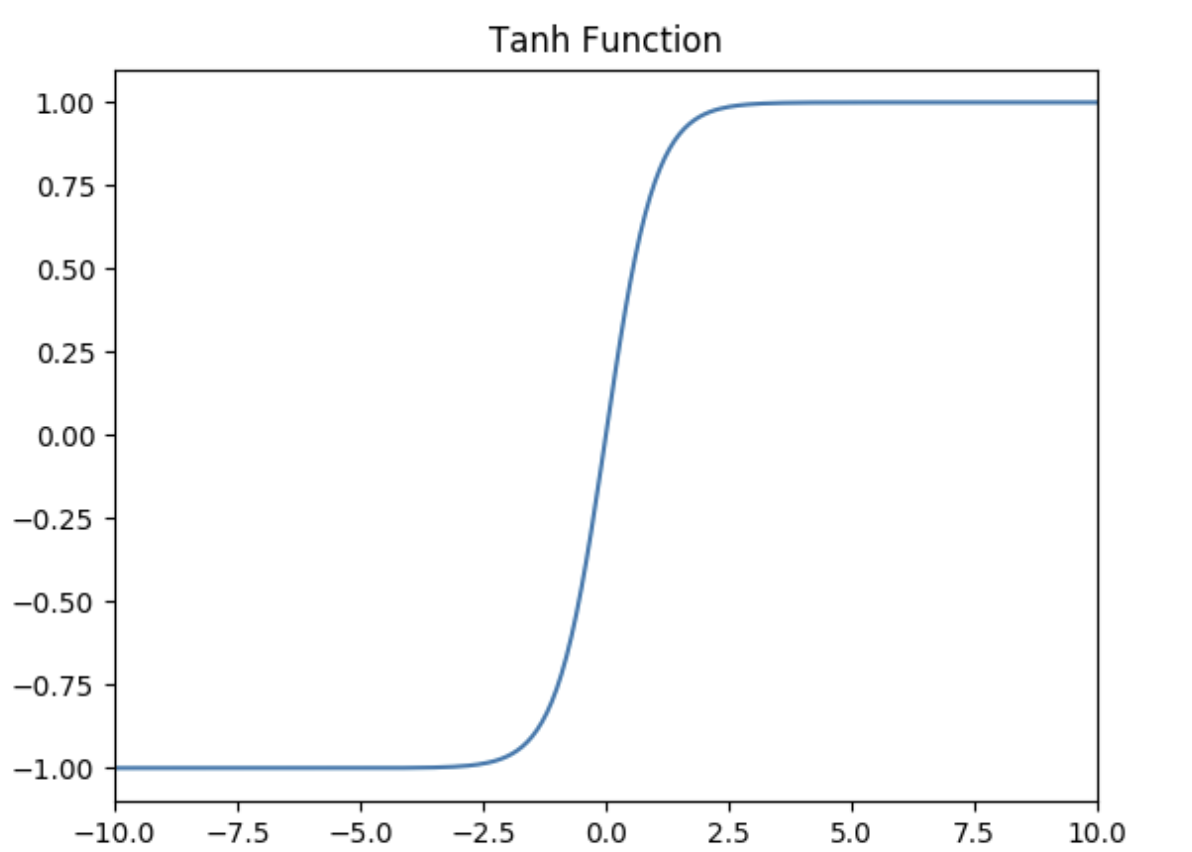
如下图所示,值域为 $(-1,1)$ 。
Tanh的优势:
1. Tanh函数把数据压缩到-1到1的范围,解决了Sigmoid函数均值不为0的问题,所以在实践中通常Tanh函数比Sigmoid函数更容易收敛。在数学形式上其实Tanh只是对Sigmoid的一个缩放形式,公式为 $tanh(x) = 2f(2x) -1$( $f(x)$ 是Sigmoid的函数)。
2. 平滑
3. 易于求导
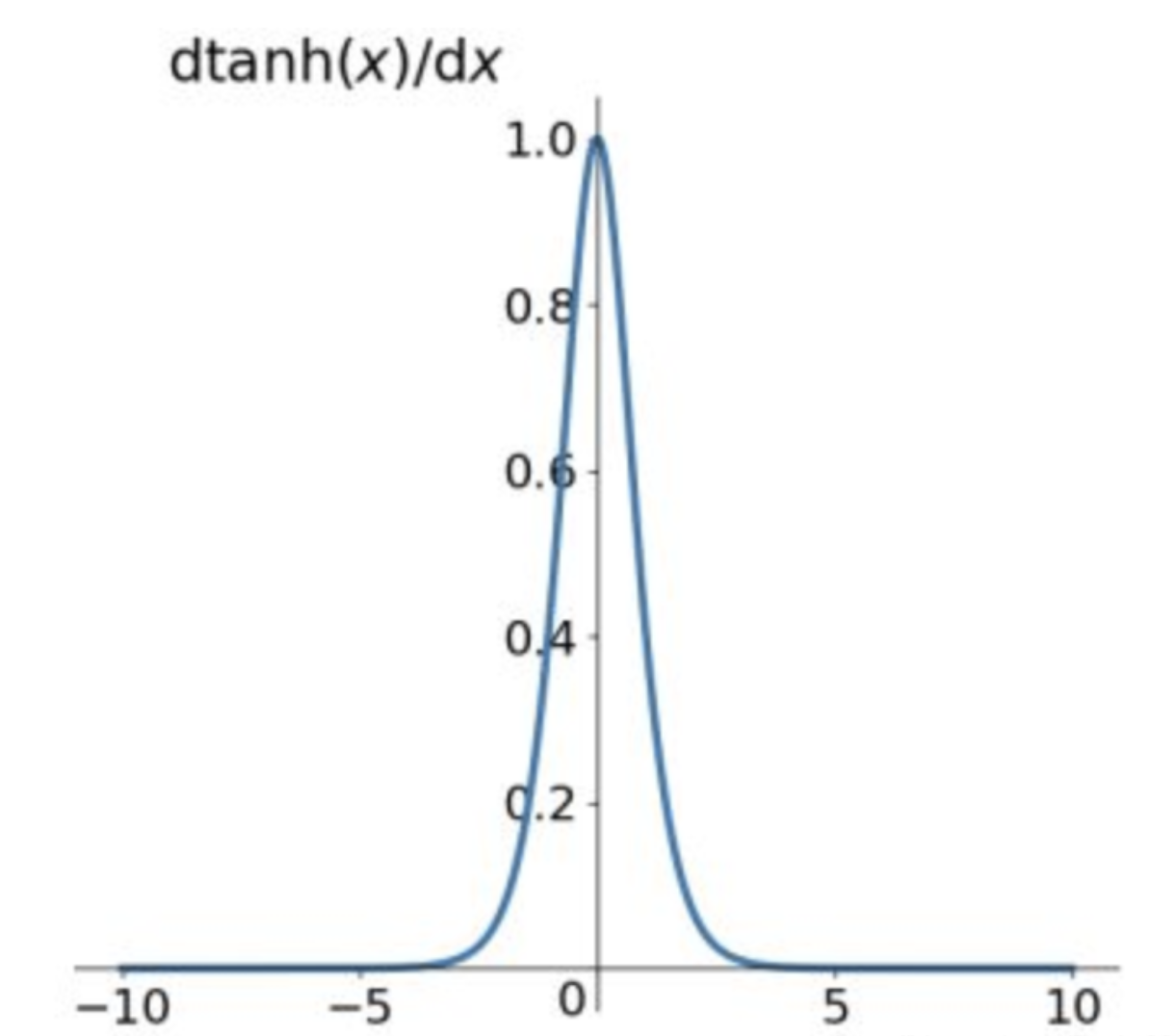
Tanh的导数:
$$f^{'}(x)=(\frac{e^x - e^{-x}}{e^x + e^{-x}})^{'}=1-(tanh(x))^2$$
当 $x=0$ 时,$f(x)'=1$ 。
由Tanh和Sigmoid的导数也可以看出Tanh导数更陡,收敛速度比Sigmoid快。
Tanh的缺点:
导数值恒小于1,反向传播易导致梯度消失。
**Relu激活函数**
Relu激活函数的定义为:
$$f(x) = max(0, x)$$
如下图所示,值域为 $[0,+∞)$ 。
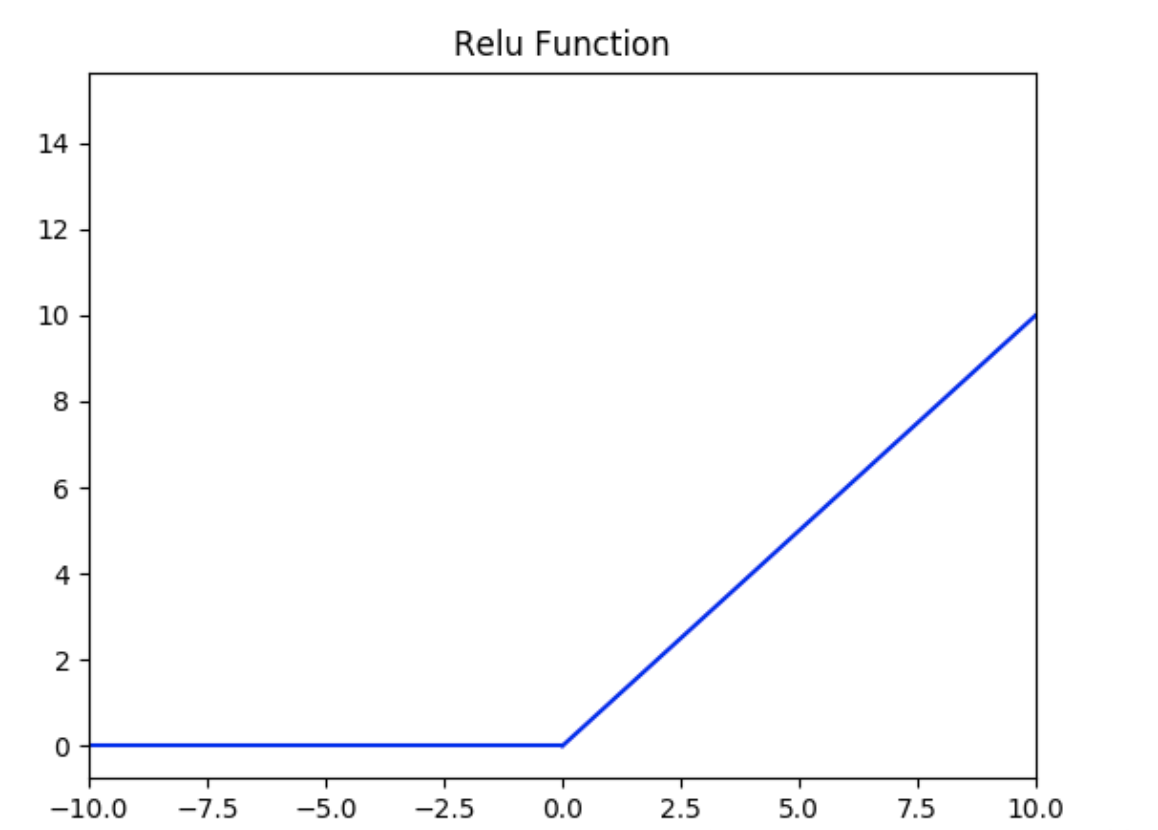
ReLU的优势:
1. 计算公式非常简单,不像上面介绍的两个激活函数那样涉及成本更高的指数运算,大量节约了计算时间。
2. 在随机梯度下降中比Sigmoid和Tanh更加容易使得网络收敛。
3. ReLU进入负半区的时候,梯度为0,神经元此时会训练形成单侧抑制,产生稀疏性,能更好更快地提取稀疏特征。
4. Sigmoid和Tanh激活函数的导数在正负饱和区的梯度都会接近于0,这会造成梯度消失,而ReLU函数大于0部分都为常数保持梯度不衰减,不会产生梯度消失现象。
稀疏:在神经网络中,这意味着激活的矩阵含有许多0。这种稀疏性能让我们得到什么?这能提升时间和空间复杂度方面的效率,常数值所需空间更少,计算成本也更低。
ReLU的导数:
$$c(u)=\begin{cases} 0,x<0 \\ 1,x>0 \\ undefined,x=0\end{cases}$$
通常 $x=0$ 时,给定其导数为 $1$ 和 $0$ 。
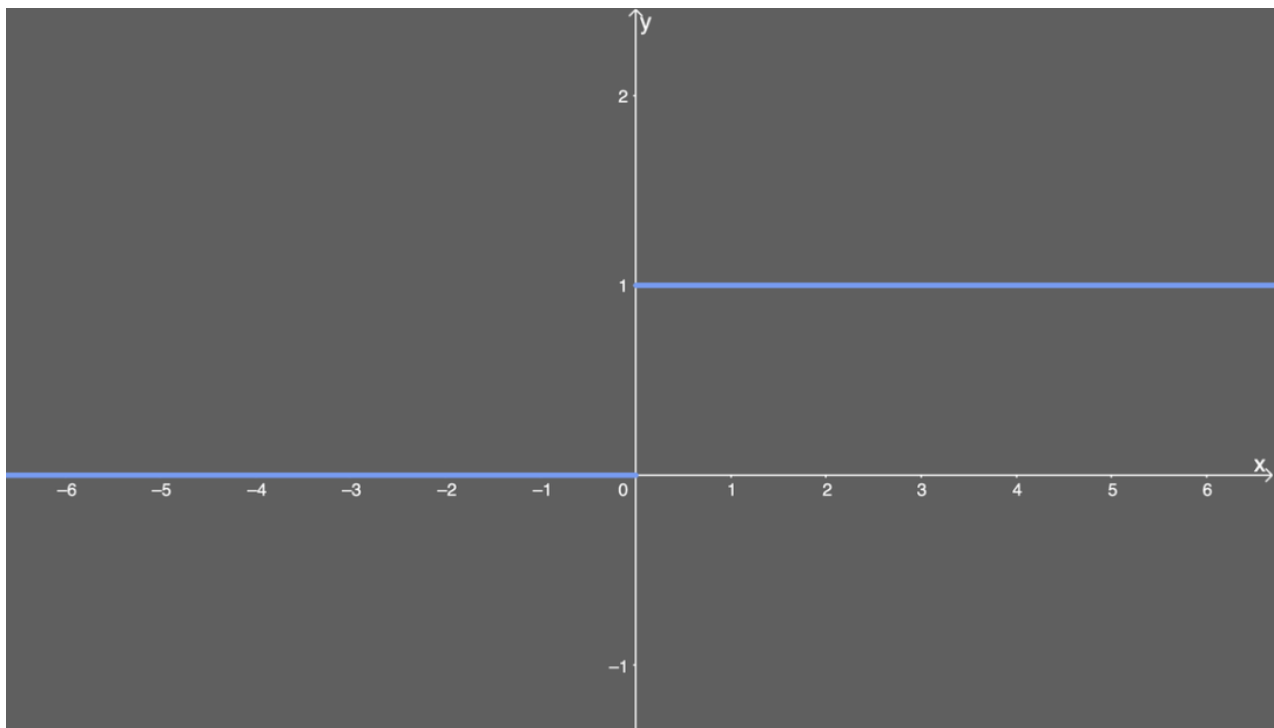
ReLU的不足:
1. 训练中可能会导致出现某些神经元永远无法更新的情况。其中一种对ReLU函数的改进方式是LeakyReLU。
2. ReLU不能避免梯度爆炸问题。
**LeakyReLU激活函数**
LeakyReLU激活函数定义为:
$$f(x) = \left\{
\begin{aligned}
ax, \quad x<0 \\
x, \quad x\ge0
\end{aligned}
\right.$$
如下图所示( $a = 0.5$ ),值域为 $(-∞,+∞)$ 。
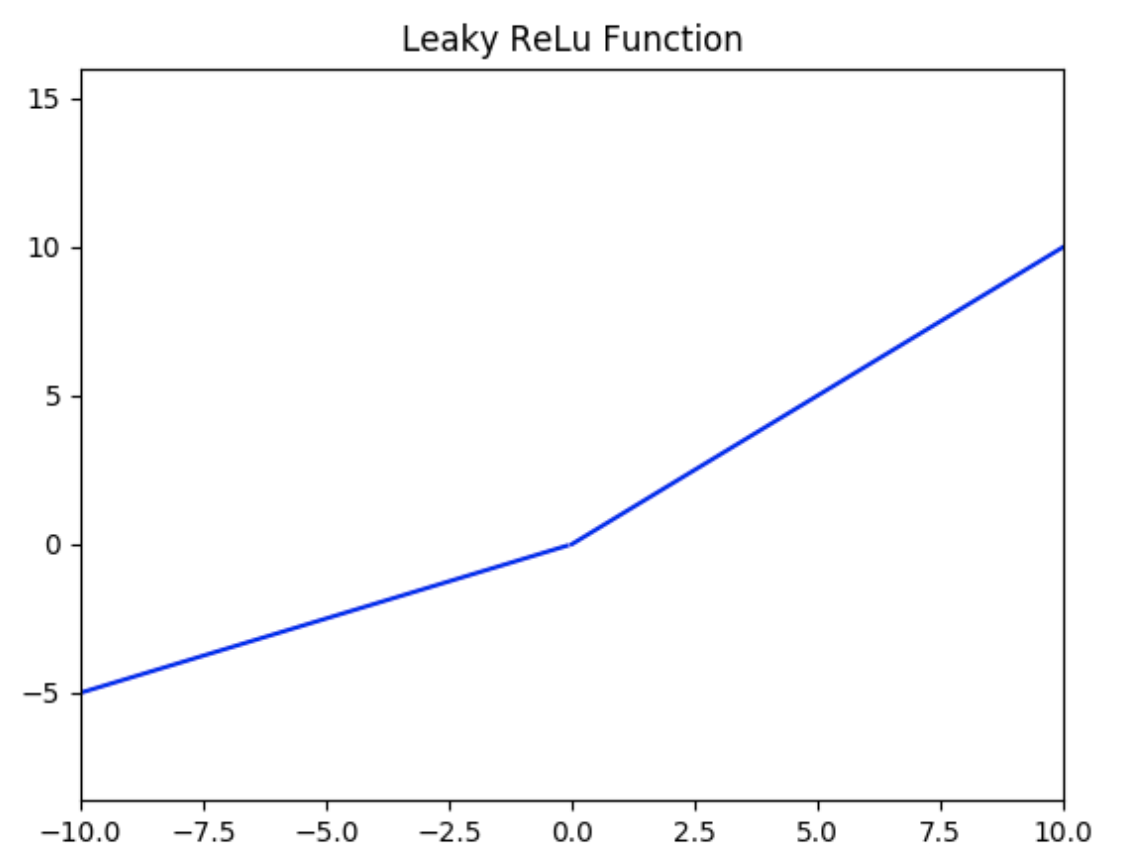
LeakyReLU的优势:
该方法与ReLU不同的是在$x$小于0的时候取 $f(x) = ax$ ,其中$a$是一个非常小的斜率(比如0.01)。这样的改进可以使得当 $x$ 小于0的时候也不会导致反向传播时的梯度消失现象。
LeakyReLU的不足:
1. 无法避免梯度爆炸的问题。
2. 神经网络不学习 $\alpha$ 值。
3. 在求导的时候,两部分都是线性的。
**SoftPlus激活函数**
SoftPlus激活函数的定义为:
$$f(x) = ln( 1 + e^x)$$
值域为 $(0,+∞)$ 。
函数图像如下:
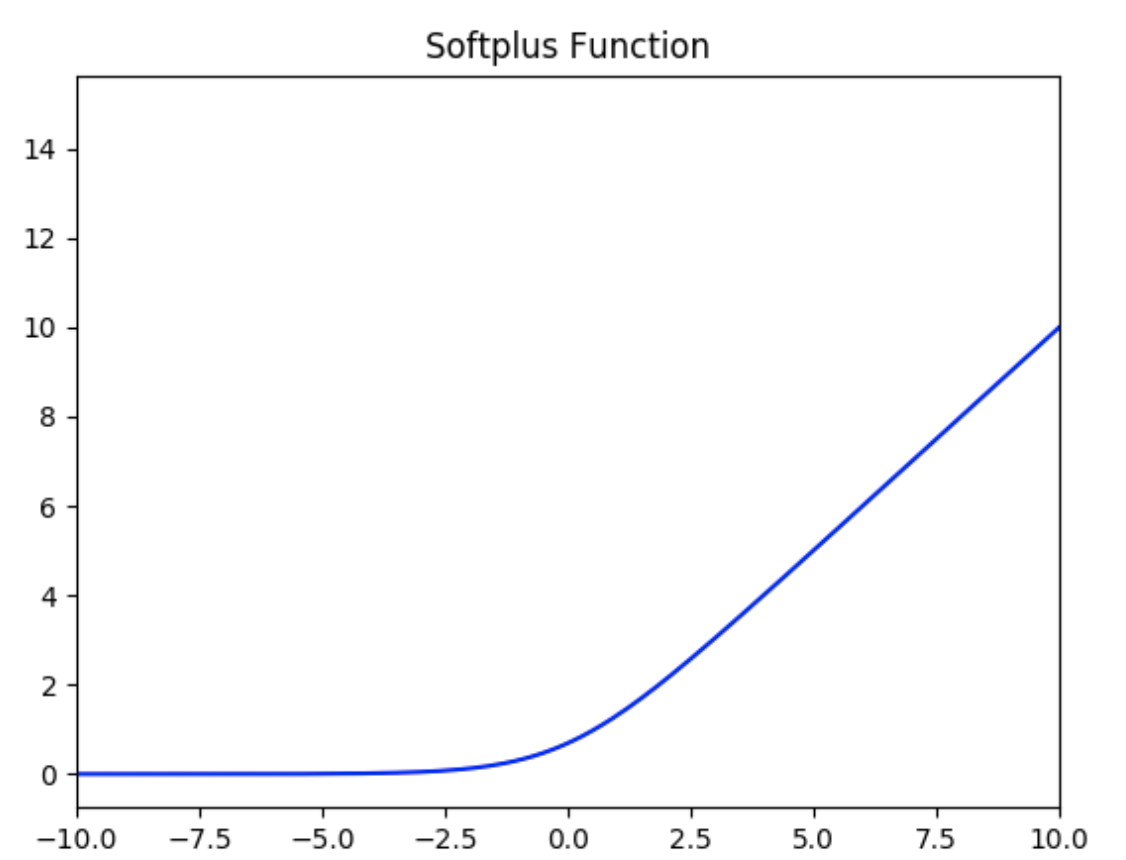
可以把SoftPlus看作是ReLU的平滑。
**ELU激活函数**
ELU激活函数解决了ReLU的一些问题,同时也保留了一些好的方面。这种激活函数要选取一个 $\alpha$ 值,其常见的取值是在0.1到0.3之间。
函数定义如下所示:
$$f(x) = \left\{
\begin{aligned}
a(e^x -1), \quad x<0 \\
x, \quad x\ge0
\end{aligned}
\right.$$
如果我们输入的 $x$ 值大于 $0$ ,则结果与ReLU一样,即 $y$ 值等于 $x$ 值;但如果输入的 $x$ 值小于 $0$ ,则我们会得到一个稍微小于 $0$ 的值,所得到的 $y$ 值取决于输入的 $x$ 值,但还要兼顾参数 $\alpha$ ——可以根据需要来调整这个参数。公式进一步引入了指数运算 $e^x$ ,因此ELU的计算成本比ReLU高。
下面给出了 $\alpha$ 值为0.2时的ELU函数图:
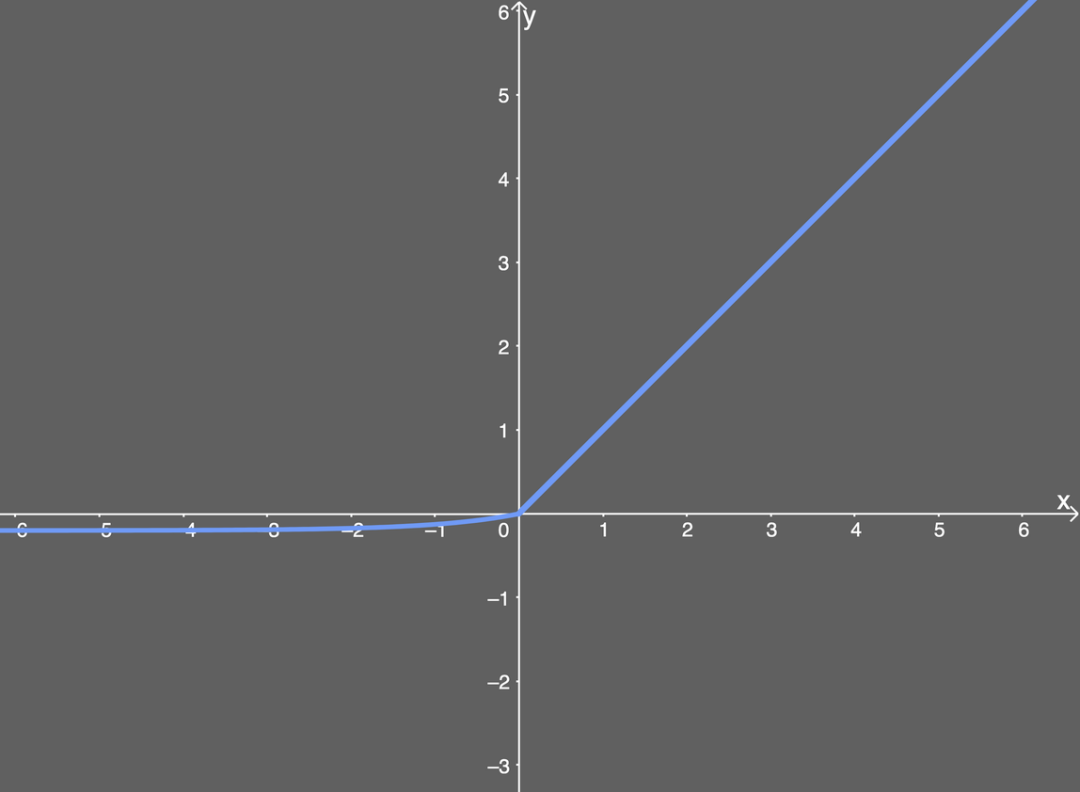
ELU的导数:
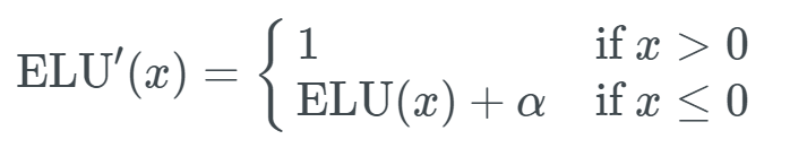
导数图如下所示:
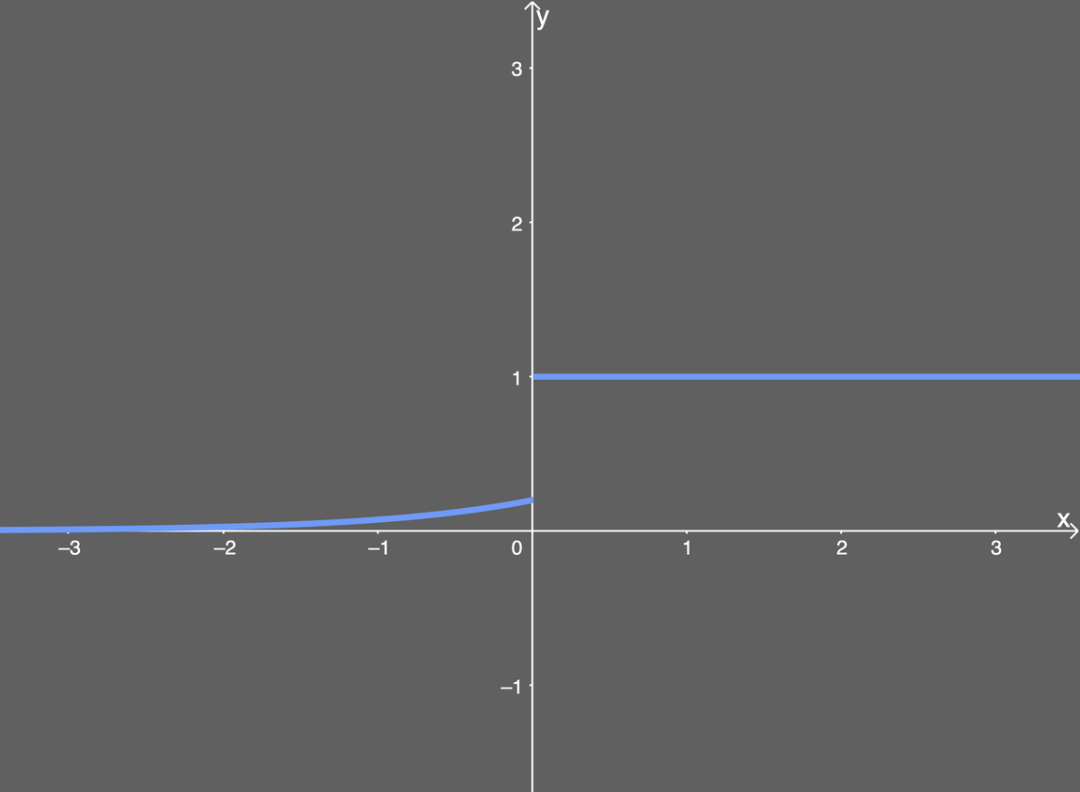
ELU的优势:
1. 能避免ReLU中一些神经元无法更新的情况。
2. 能得到负值输出。
ELU的不足:
1. 包含指数运算,计算时间长。
2. 无法避免梯度爆炸问题。
3. 神经网络无法学习 $\alpha$ 值。
首先我们看一下GELU激活函数的公式:
$$GELU(x) = 0.5 \times x \times \left(1 + \tanh\left(\sqrt{\frac{2}{\pi}} \times \left(x + 0.044715 \times x^3\right)\right)\right)$$
了解了GELU激活函数的计算机制后,我们再将其与经典的ReLU激活函数、Sigmoid激活函数进行比较,能够更好的理解GELU激活函数的优势,下面是三者的对比图:
其中 x 代表输入的网络权重参数。
假设我们设置输入值为 x=1.0,最终可以得到GELU激活函数的输出值为:
$$GELU(1.0) = 0.5 \times 1.0 \times (1 + 0.683675) = 0.5 \times 1.0 \times 1.683675 \approx 0.8418375$$
了解了GELU激活函数的计算机制后,我们再将其与经典的ReLU激活函数、Sigmoid激活函数进行比较,能够更好的理解GELU激活函数的优势,下面是三者的对比图:

从上图可以看出:
1. ReLU激活函数在输入为正数时,输出与输入相同;在输入为负数时,输出为0。它非常简单但会完全忽略负值的输入。
2. Sigmoid激活函数输出在 0 到 1 之间平滑过渡,适合在某些分类任务中使用,但可能会导致梯度消失问题。
3. GELU激活函数比 ReLU 更平滑,并且在负值附近不会直接剪切到 0。它让负值小幅保留,避免了完全忽略负输入,同时保留了 ReLU 在正值区间的主要优点。
总的来说,**GELU是一种更平滑的激活函数,能更好地保留输入的细微信息,尤其是在处理负值时。通过结合多种非线性运算(如 tanh 和多项式),GELU 提供了比 ReLU 更平滑和复杂的输出,有助于AI模型在训练过程中更好地捕捉数据中的复杂特征与模式**。
SiLU激活函数全称为 Sigmoid Linear Unit,是一种结合了线性和非线性特性的激活函数,也是Swish激活函数的一种特殊形式。**它是一种非线性激活函数,用于神经网络的各层之间,以引入非线性,从而使神经网络能够学习更复杂的模式和特征**。
### SiLU 激活函数的定义
SiLU 函数的数学定义如下:
$$\text{SiLU}(x) = x \cdot \sigma(x)$$
其中:
- $x$ 是输入张量。
- $\sigma(x)$ 是输入的 Sigmoid 函数,即:
$$\sigma(x) = \frac{1}{1 + e^{-x}}$$
因此,SiLU 函数可以被表达为:
$$\text{SiLU}(x) = \frac{x}{1 + e^{-x}}$$
下面是SiLU激活函数的示意图:

### SiLU 函数的特性
1. **平滑性**:SiLU 是一个平滑的函数,它不像 ReLU 那样在原点处有一个“拐角”,而是具有光滑的过渡,这对优化过程可能更有利。
2. **非线性**:SiLU 是非线性的,允许模型学习复杂的模式。这也是所有激活函数的核心属性。
3. **无界性**:SiLU 是无界的(即它的输出可以任意大),这与 ReLU 类似,但不同于 Sigmoid 或 Tanh 这类函数(它们的输出是有界的)。
4. **有梯度消失的风险**:虽然 SiLU 的输出范围是无界的,但对于负值输入,其输出接近零,因此在深度网络的训练中可能存在类似于 ReLU 的梯度消失问题,但通常比 ReLU 要好一些,因为它的负值部分并不是完全归零,而是有少量的负梯度。
### SiLU 与其他激活函数相比的优势
- **与 ReLU 的比较**:ReLU 函数(即 $\text{ReLU}(x) = \max(0, x)$ )在负值时输出为零,而 SiLU 在负值时输出为负,但仍保留了一定的梯度,这在某些情况下可以改进梯度流动的问题。
- **与 Sigmoid 的比较**:Sigmoid 函数输出值在 0 到 1 之间,而 SiLU 保持了输入的线性部分,因此在正值范围内表现出更大的动态范围。
- **与 Swish 的关系**:SiLU 实际上就是 Swish 函数的一个特殊形式。Swish 函数通常被定义为 $\text{Swish}(x) = x \cdot \sigma(\beta x)$ ,其中 $\beta$ 是一个可调参数。当 $\beta = 1$ 时,Swish 就变成了 SiLU。
**NewGELU** 是对传统 **GELU (Gaussian Error Linear Unit)** 的一种改进。GELU 本身在许多AI模型中表现优异(如 Transformer 系列模型),而 NewGELU 在保留 GELU 平滑特性的同时,进一步优化了计算效率和非线性特性,从而可以在一些AI任务中获得更好的表现。
## 一、GELU 激活函数的回顾
在了解 NewGELU 之前,我们先回顾一下 GELU 激活函数的定义和特点,以便更好地理解 NewGELU 的改进之处。
### 1. **GELU 的数学定义**
GELU 激活函数的数学表达式为:
$$
\text{GELU}(x) = x \cdot \Phi(x)
$$
其中, $\Phi(x)$ 是标准正态分布的累积分布函数(CDF),定义为:
$$
\Phi(x) = \frac{1}{2} \left(1 + \text{erf}\left(\frac{x}{\sqrt{2}}\right)\right)
$$
由于累积分布函数的计算较为复杂,GELU 常使用以下近似表达式来加速计算:
$$
\text{GELU}(x) \approx 0.5 \cdot x \cdot \left(1 + \tanh\left(\sqrt{\frac{2}{\pi}} \left( x + 0.044715 \cdot x^3 \right)\right)\right)
$$
### 2. **GELU 的特点**
- **平滑性**:GELU 是连续可导的函数,使得梯度流动更加顺畅。
- **概率性**:GELU 基于输入值的大小概率性地保留或抑制输入,从而实现了平滑的门控效果。
- **性能**:在许多AI模型中,如 BERT、GPT 等,GELU 显著优于 ReLU、Tanh 等传统激活函数。
## 二、NewGELU 的引入
**NewGELU** 是一种对 GELU 的改进,其目标是:
1. **优化计算效率**:通过更简洁的公式减少计算量。
2. **改善模型性能**:在保持 GELU 平滑特性的同时,进一步提升深度学习模型的表现。
## 三、NewGELU 激活函数的定义
### 1. **数学表达式**
NewGELU 激活函数的近似表达式为:
$$
\text{NewGELU}(x) = 0.5 \cdot x \cdot \left(1 + \tanh\left(\sqrt{\frac{2}{\pi}} \cdot (x + 0.0356774 \cdot x^3)\right)\right)
$$
与 GELU 的近似表达式对比:
$$
\text{GELU}(x) \approx 0.5 \cdot x \cdot \left(1 + \tanh\left(\sqrt{\frac{2}{\pi}} \left( x + 0.044715 \cdot x^3 \right)\right)\right)
$$
### 2. **公式的简化**
NewGELU 的公式与 GELU 非常相似,但将常数 `0.044715` 改为 `0.0356774`。这一小小的改动,使得 NewGELU 在计算上更加高效,且在某些任务中表现略优于标准 GELU。
## 四、NewGELU 的特性
### 1. **更高的计算效率**
- NewGELU 通过调整公式中的系数,减少了计算复杂度,特别是在模型推理时表现出色。
- 虽然调整系数的幅度很小,但这对计算量较大的深度学习模型来说可以带来实际的性能提升。
### 2. **平滑的非线性**
- 与 GELU 一样,NewGELU 也是连续可导的,并且具有平滑的曲线。这样的非线性特性对深层网络中的梯度流动非常友好。
- **负值区域**:在负值区域,NewGELU 的输出逐渐接近于零,但并不会像 ReLU 那样直接截断为零,因此可以保留一部分负值信息。
### 3. **自适应性**
- NewGELU 的自适应性体现在它对不同大小的输入值可以进行“自门控”。大输入值的激活值接近于输入值,而小输入值的激活值则接近于零。
- 这种特性类似于“概率门控”,能够在保持输入特征完整性的同时,抑制噪声和无关信息。
## 五、总结
- **NewGELU** 是对 GELU 激活函数的改进,通过简化公式并优化常数项,使得计算效率更高。
- **特点**:具有平滑过渡、负值信息保留、自门控等特性,适用于各种深度学习模型。
- **应用场景**:Transformer、CNN、强化学习等任务中,NewGELU 提供了更好的梯度流动和模型收敛性能。
- **实验结果**:在 NLP 和图像任务中,新型模型往往采用 NewGELU,以提升模型的训练速度和准确率。
计算公式:GeLU(x) = x Φ(x)
这里Φ ( x ) 是标准正态分布的累积分布函数,可以简单采用正态分布N ( 0 , 1 ) , 当然可以使用参数化的正态分布N ( μ , σ ) , 然后通过训练得到μ , σ 。
假设输入是一个标量 x,假设为标准正态分布的GELU(x), 近似计算的数学公式:
GeLU(x) = 0.5 * x * (1 + tanh(sqrt(2 / pi) * (x + 0.044715 * x^3)))
其中,tanh() 是双曲正切函数,sqrt() 是平方根函数,pi 是圆周率。
非线形激活函数,应用于 FFN块。实现了非线性加上泛化,特别占内存,计算量很大
特点:在小于0的输入接近0(非线性),在大于0的输入上接近线性函数
优点:相比ReLU,更平滑,更快的收敛速度。(依赖于正态分布的性质)
缺点:计算复杂度较高,可能会增加模型的计算开销。
计算公式:Swish(x) = x * sigmoid(betax)
其中,sigmoid() 是Sigmoid函数,x 是输入,beta 是一个可调节的超参数。当beta为0时,Swish函数退化为线性函数;当beta趋近于无穷大时,Swish函数趋近于ReLU函数。
非线形激活函数,应用于 FFN块。在ReLU的优势基础上强化了门控机制,超参数β的加入使得函数可以调整门控的开关状态来近似于不同的ReLU函数。
● 继承了ReLU的优势,在X>0时依然不存在梯度消失问题。
● 同时<0的部分也不会轻易的死亡,门控机制的加入使得灵活性变强。
● β参数可以唯一也可以该层每个神经元各对应一个。(一对一学习,一对多进行固定)
特点:在小于0的输入接近0(非线性),在大于0的输入上接近线性函数
优点:相比ReLU,更平滑,更快的收敛速度。(依赖于正态分布的性质)
缺点:计算开销较大,因为它需要进行Sigmoid运算。
- [1.激活函数的作用,常用的激活函数有哪些](#user-content-1激活函数的作用,常用的激活函数有哪些)
- [2.什么是GELU激活函数?](#user-content-2什么是GELU激活函数?)
- [3.什么是SiLU激活函数?](#user-content-3什么是SiLU激活函数?)
- [4.什么是NewGELU激活函数?](#user-content-4什么是NewGELU激活函数?)
- [5.介绍一下 GeLU 计算公式?](#user-content-5.介绍一下GeLU计算公式?)
- [6.介绍一下 Swish 计算公式?](#user-content-6.介绍一下Swish计算公式?)
1.激活函数的作用,常用的激活函数有哪些
### 激活函数的作用
激活函数可以引入非线性因素,提升网络的学习表达能力。
### 常用的激活函数
**Sigmoid 激活函数**
函数的定义为:
$$f(x) = \frac{1}{1 + e^{-x}}$$
如下图所示,其值域为 $(0,1)$ 。也就是说,输入的每个神经元、节点都会被缩放到一个介于 $0$ 和 $1$ 之间的值。
当 $x$ 大于零时输出结果会趋近于 $1$ ,而当 $x$ 小于零时,输出结果趋向于 $0$ ,由于函数的特性,经常被用作二分类的输出端激活函数。

Sigmoid的导数:
$$f^{'}(x)=(\frac{1}{1+e^{-x}})^{'}=\frac{1}{1+e^{-x}}\left( 1- \frac{1}{1+e^{-x}} \right)=f(x)(1-f(x))$$
当 $x=0$ 时, $f(x)'=0.25$ 。
Sigmoid的优点:
1. 平滑
2. 易于求导
3. 可以作为概率,辅助解释模型的输出结果
Sigmoid的缺陷:
1. 当输入数据很大或者很小时,函数的梯度几乎接近于0,这对神经网络在反向传播中的学习非常不利。
2. Sigmoid函数的均值不是0,这使得神经网络的训练过程中只会产生全正或全负的反馈。
3. 导数值恒小于1,反向传播易导致梯度消失。

**Tanh激活函数**
Tanh函数的定义为:
$$f(x) = Tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$$
如下图所示,值域为 $(-1,1)$ 。

Tanh的优势:
1. Tanh函数把数据压缩到-1到1的范围,解决了Sigmoid函数均值不为0的问题,所以在实践中通常Tanh函数比Sigmoid函数更容易收敛。在数学形式上其实Tanh只是对Sigmoid的一个缩放形式,公式为 $tanh(x) = 2f(2x) -1$( $f(x)$ 是Sigmoid的函数)。
2. 平滑
3. 易于求导
Tanh的导数:
$$f^{'}(x)=(\frac{e^x - e^{-x}}{e^x + e^{-x}})^{'}=1-(tanh(x))^2$$
当 $x=0$ 时,$f(x)'=1$ 。
由Tanh和Sigmoid的导数也可以看出Tanh导数更陡,收敛速度比Sigmoid快。

Tanh的缺点:
导数值恒小于1,反向传播易导致梯度消失。
**Relu激活函数**
Relu激活函数的定义为:
$$f(x) = max(0, x)$$
如下图所示,值域为 $[0,+∞)$ 。

ReLU的优势:
1. 计算公式非常简单,不像上面介绍的两个激活函数那样涉及成本更高的指数运算,大量节约了计算时间。
2. 在随机梯度下降中比Sigmoid和Tanh更加容易使得网络收敛。
3. ReLU进入负半区的时候,梯度为0,神经元此时会训练形成单侧抑制,产生稀疏性,能更好更快地提取稀疏特征。
4. Sigmoid和Tanh激活函数的导数在正负饱和区的梯度都会接近于0,这会造成梯度消失,而ReLU函数大于0部分都为常数保持梯度不衰减,不会产生梯度消失现象。
稀疏:在神经网络中,这意味着激活的矩阵含有许多0。这种稀疏性能让我们得到什么?这能提升时间和空间复杂度方面的效率,常数值所需空间更少,计算成本也更低。
ReLU的导数:
$$c(u)=\begin{cases} 0,x<0 \\ 1,x>0 \\ undefined,x=0\end{cases}$$
通常 $x=0$ 时,给定其导数为 $1$ 和 $0$ 。

ReLU的不足:
1. 训练中可能会导致出现某些神经元永远无法更新的情况。其中一种对ReLU函数的改进方式是LeakyReLU。
2. ReLU不能避免梯度爆炸问题。
**LeakyReLU激活函数**
LeakyReLU激活函数定义为:
$$f(x) = \left\{
\begin{aligned}
ax, \quad x<0 \\
x, \quad x\ge0
\end{aligned}
\right.$$
如下图所示( $a = 0.5$ ),值域为 $(-∞,+∞)$ 。

LeakyReLU的优势:
该方法与ReLU不同的是在$x$小于0的时候取 $f(x) = ax$ ,其中$a$是一个非常小的斜率(比如0.01)。这样的改进可以使得当 $x$ 小于0的时候也不会导致反向传播时的梯度消失现象。
LeakyReLU的不足:
1. 无法避免梯度爆炸的问题。
2. 神经网络不学习 $\alpha$ 值。
3. 在求导的时候,两部分都是线性的。
**SoftPlus激活函数**
SoftPlus激活函数的定义为:
$$f(x) = ln( 1 + e^x)$$
值域为 $(0,+∞)$ 。
函数图像如下:

可以把SoftPlus看作是ReLU的平滑。
**ELU激活函数**
ELU激活函数解决了ReLU的一些问题,同时也保留了一些好的方面。这种激活函数要选取一个 $\alpha$ 值,其常见的取值是在0.1到0.3之间。
函数定义如下所示:
$$f(x) = \left\{
\begin{aligned}
a(e^x -1), \quad x<0 \\
x, \quad x\ge0
\end{aligned}
\right.$$
如果我们输入的 $x$ 值大于 $0$ ,则结果与ReLU一样,即 $y$ 值等于 $x$ 值;但如果输入的 $x$ 值小于 $0$ ,则我们会得到一个稍微小于 $0$ 的值,所得到的 $y$ 值取决于输入的 $x$ 值,但还要兼顾参数 $\alpha$ ——可以根据需要来调整这个参数。公式进一步引入了指数运算 $e^x$ ,因此ELU的计算成本比ReLU高。
下面给出了 $\alpha$ 值为0.2时的ELU函数图:

ELU的导数:
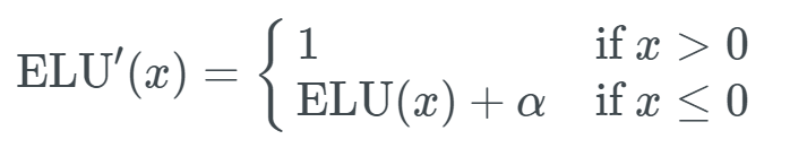
导数图如下所示:

ELU的优势:
1. 能避免ReLU中一些神经元无法更新的情况。
2. 能得到负值输出。
ELU的不足:
1. 包含指数运算,计算时间长。
2. 无法避免梯度爆炸问题。
3. 神经网络无法学习 $\alpha$ 值。
2.什么是GELU激活函数?
首先我们看一下GELU激活函数的公式:
$$GELU(x) = 0.5 \times x \times \left(1 + \tanh\left(\sqrt{\frac{2}{\pi}} \times \left(x + 0.044715 \times x^3\right)\right)\right)$$
了解了GELU激活函数的计算机制后,我们再将其与经典的ReLU激活函数、Sigmoid激活函数进行比较,能够更好的理解GELU激活函数的优势,下面是三者的对比图:
其中 x 代表输入的网络权重参数。
假设我们设置输入值为 x=1.0,最终可以得到GELU激活函数的输出值为:
$$GELU(1.0) = 0.5 \times 1.0 \times (1 + 0.683675) = 0.5 \times 1.0 \times 1.683675 \approx 0.8418375$$
了解了GELU激活函数的计算机制后,我们再将其与经典的ReLU激活函数、Sigmoid激活函数进行比较,能够更好的理解GELU激活函数的优势,下面是三者的对比图:

从上图可以看出:
1. ReLU激活函数在输入为正数时,输出与输入相同;在输入为负数时,输出为0。它非常简单但会完全忽略负值的输入。
2. Sigmoid激活函数输出在 0 到 1 之间平滑过渡,适合在某些分类任务中使用,但可能会导致梯度消失问题。
3. GELU激活函数比 ReLU 更平滑,并且在负值附近不会直接剪切到 0。它让负值小幅保留,避免了完全忽略负输入,同时保留了 ReLU 在正值区间的主要优点。
总的来说,**GELU是一种更平滑的激活函数,能更好地保留输入的细微信息,尤其是在处理负值时。通过结合多种非线性运算(如 tanh 和多项式),GELU 提供了比 ReLU 更平滑和复杂的输出,有助于AI模型在训练过程中更好地捕捉数据中的复杂特征与模式**。
3.什么是SiLU激活函数?
SiLU激活函数全称为 Sigmoid Linear Unit,是一种结合了线性和非线性特性的激活函数,也是Swish激活函数的一种特殊形式。**它是一种非线性激活函数,用于神经网络的各层之间,以引入非线性,从而使神经网络能够学习更复杂的模式和特征**。
### SiLU 激活函数的定义
SiLU 函数的数学定义如下:
$$\text{SiLU}(x) = x \cdot \sigma(x)$$
其中:
- $x$ 是输入张量。
- $\sigma(x)$ 是输入的 Sigmoid 函数,即:
$$\sigma(x) = \frac{1}{1 + e^{-x}}$$
因此,SiLU 函数可以被表达为:
$$\text{SiLU}(x) = \frac{x}{1 + e^{-x}}$$
下面是SiLU激活函数的示意图:

### SiLU 函数的特性
1. **平滑性**:SiLU 是一个平滑的函数,它不像 ReLU 那样在原点处有一个“拐角”,而是具有光滑的过渡,这对优化过程可能更有利。
2. **非线性**:SiLU 是非线性的,允许模型学习复杂的模式。这也是所有激活函数的核心属性。
3. **无界性**:SiLU 是无界的(即它的输出可以任意大),这与 ReLU 类似,但不同于 Sigmoid 或 Tanh 这类函数(它们的输出是有界的)。
4. **有梯度消失的风险**:虽然 SiLU 的输出范围是无界的,但对于负值输入,其输出接近零,因此在深度网络的训练中可能存在类似于 ReLU 的梯度消失问题,但通常比 ReLU 要好一些,因为它的负值部分并不是完全归零,而是有少量的负梯度。
### SiLU 与其他激活函数相比的优势
- **与 ReLU 的比较**:ReLU 函数(即 $\text{ReLU}(x) = \max(0, x)$ )在负值时输出为零,而 SiLU 在负值时输出为负,但仍保留了一定的梯度,这在某些情况下可以改进梯度流动的问题。
- **与 Sigmoid 的比较**:Sigmoid 函数输出值在 0 到 1 之间,而 SiLU 保持了输入的线性部分,因此在正值范围内表现出更大的动态范围。
- **与 Swish 的关系**:SiLU 实际上就是 Swish 函数的一个特殊形式。Swish 函数通常被定义为 $\text{Swish}(x) = x \cdot \sigma(\beta x)$ ,其中 $\beta$ 是一个可调参数。当 $\beta = 1$ 时,Swish 就变成了 SiLU。
4.什么是NewGELU激活函数?
**NewGELU** 是对传统 **GELU (Gaussian Error Linear Unit)** 的一种改进。GELU 本身在许多AI模型中表现优异(如 Transformer 系列模型),而 NewGELU 在保留 GELU 平滑特性的同时,进一步优化了计算效率和非线性特性,从而可以在一些AI任务中获得更好的表现。
## 一、GELU 激活函数的回顾
在了解 NewGELU 之前,我们先回顾一下 GELU 激活函数的定义和特点,以便更好地理解 NewGELU 的改进之处。
### 1. **GELU 的数学定义**
GELU 激活函数的数学表达式为:
$$
\text{GELU}(x) = x \cdot \Phi(x)
$$
其中, $\Phi(x)$ 是标准正态分布的累积分布函数(CDF),定义为:
$$
\Phi(x) = \frac{1}{2} \left(1 + \text{erf}\left(\frac{x}{\sqrt{2}}\right)\right)
$$
由于累积分布函数的计算较为复杂,GELU 常使用以下近似表达式来加速计算:
$$
\text{GELU}(x) \approx 0.5 \cdot x \cdot \left(1 + \tanh\left(\sqrt{\frac{2}{\pi}} \left( x + 0.044715 \cdot x^3 \right)\right)\right)
$$
### 2. **GELU 的特点**
- **平滑性**:GELU 是连续可导的函数,使得梯度流动更加顺畅。
- **概率性**:GELU 基于输入值的大小概率性地保留或抑制输入,从而实现了平滑的门控效果。
- **性能**:在许多AI模型中,如 BERT、GPT 等,GELU 显著优于 ReLU、Tanh 等传统激活函数。
## 二、NewGELU 的引入
**NewGELU** 是一种对 GELU 的改进,其目标是:
1. **优化计算效率**:通过更简洁的公式减少计算量。
2. **改善模型性能**:在保持 GELU 平滑特性的同时,进一步提升深度学习模型的表现。
## 三、NewGELU 激活函数的定义
### 1. **数学表达式**
NewGELU 激活函数的近似表达式为:
$$
\text{NewGELU}(x) = 0.5 \cdot x \cdot \left(1 + \tanh\left(\sqrt{\frac{2}{\pi}} \cdot (x + 0.0356774 \cdot x^3)\right)\right)
$$
与 GELU 的近似表达式对比:
$$
\text{GELU}(x) \approx 0.5 \cdot x \cdot \left(1 + \tanh\left(\sqrt{\frac{2}{\pi}} \left( x + 0.044715 \cdot x^3 \right)\right)\right)
$$
### 2. **公式的简化**
NewGELU 的公式与 GELU 非常相似,但将常数 `0.044715` 改为 `0.0356774`。这一小小的改动,使得 NewGELU 在计算上更加高效,且在某些任务中表现略优于标准 GELU。
## 四、NewGELU 的特性
### 1. **更高的计算效率**
- NewGELU 通过调整公式中的系数,减少了计算复杂度,特别是在模型推理时表现出色。
- 虽然调整系数的幅度很小,但这对计算量较大的深度学习模型来说可以带来实际的性能提升。
### 2. **平滑的非线性**
- 与 GELU 一样,NewGELU 也是连续可导的,并且具有平滑的曲线。这样的非线性特性对深层网络中的梯度流动非常友好。
- **负值区域**:在负值区域,NewGELU 的输出逐渐接近于零,但并不会像 ReLU 那样直接截断为零,因此可以保留一部分负值信息。
### 3. **自适应性**
- NewGELU 的自适应性体现在它对不同大小的输入值可以进行“自门控”。大输入值的激活值接近于输入值,而小输入值的激活值则接近于零。
- 这种特性类似于“概率门控”,能够在保持输入特征完整性的同时,抑制噪声和无关信息。
## 五、总结
- **NewGELU** 是对 GELU 激活函数的改进,通过简化公式并优化常数项,使得计算效率更高。
- **特点**:具有平滑过渡、负值信息保留、自门控等特性,适用于各种深度学习模型。
- **应用场景**:Transformer、CNN、强化学习等任务中,NewGELU 提供了更好的梯度流动和模型收敛性能。
- **实验结果**:在 NLP 和图像任务中,新型模型往往采用 NewGELU,以提升模型的训练速度和准确率。
5.介绍一下 GeLU 计算公式?
计算公式:GeLU(x) = x Φ(x)
这里Φ ( x ) 是标准正态分布的累积分布函数,可以简单采用正态分布N ( 0 , 1 ) , 当然可以使用参数化的正态分布N ( μ , σ ) , 然后通过训练得到μ , σ 。
假设输入是一个标量 x,假设为标准正态分布的GELU(x), 近似计算的数学公式:
GeLU(x) = 0.5 * x * (1 + tanh(sqrt(2 / pi) * (x + 0.044715 * x^3)))
其中,tanh() 是双曲正切函数,sqrt() 是平方根函数,pi 是圆周率。
非线形激活函数,应用于 FFN块。实现了非线性加上泛化,特别占内存,计算量很大
特点:在小于0的输入接近0(非线性),在大于0的输入上接近线性函数
优点:相比ReLU,更平滑,更快的收敛速度。(依赖于正态分布的性质)
缺点:计算复杂度较高,可能会增加模型的计算开销。
6.介绍一下 Swish 计算公式?
计算公式:Swish(x) = x * sigmoid(betax)
其中,sigmoid() 是Sigmoid函数,x 是输入,beta 是一个可调节的超参数。当beta为0时,Swish函数退化为线性函数;当beta趋近于无穷大时,Swish函数趋近于ReLU函数。
非线形激活函数,应用于 FFN块。在ReLU的优势基础上强化了门控机制,超参数β的加入使得函数可以调整门控的开关状态来近似于不同的ReLU函数。
● 继承了ReLU的优势,在X>0时依然不存在梯度消失问题。
● 同时<0的部分也不会轻易的死亡,门控机制的加入使得灵活性变强。
● β参数可以唯一也可以该层每个神经元各对应一个。(一对一学习,一对多进行固定)
特点:在小于0的输入接近0(非线性),在大于0的输入上接近线性函数
优点:相比ReLU,更平滑,更快的收敛速度。(依赖于正态分布的性质)
缺点:计算开销较大,因为它需要进行Sigmoid运算。
点赞
回复
X